题目内容
抛物线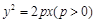 的焦点为
的焦点为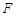 ,过焦点
,过焦点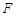 倾斜角为
倾斜角为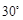 的直线交抛物线于
的直线交抛物线于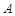 ,
,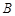 两点,点
两点,点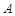 ,
,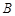 在抛物线准线上的射影分别是
在抛物线准线上的射影分别是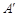 ,
,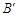 ,若四边形
,若四边形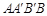 的面积为
的面积为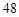 ,则抛物线的方程为____
,则抛物线的方程为____
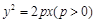 的焦点为
的焦点为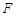 ,过焦点
,过焦点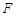 倾斜角为
倾斜角为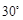 的直线交抛物线于
的直线交抛物线于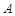 ,
,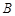 两点,点
两点,点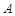 ,
,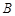 在抛物线准线上的射影分别是
在抛物线准线上的射影分别是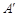 ,
,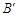 ,若四边形
,若四边形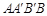 的面积为
的面积为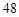 ,则抛物线的方程为____
,则抛物线的方程为____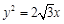
试题分析:抛物线的焦点为F(
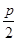 ,0),所以直线AB的方程为
,0),所以直线AB的方程为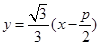 ,代入
,代入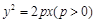 ,整理得,
,整理得,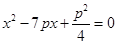 。
。设A
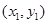 ,B
,B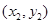 ,则由韦达定理得,
,则由韦达定理得,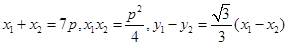 ,
,又四边形
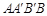 是梯形,其面积为
是梯形,其面积为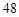 ,所以,
,所以,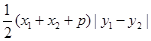 =48,
=48,即,
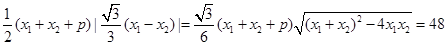 ,
,解得,
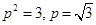 ,故答案为
,故答案为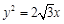 。
。点评:中档题,本题综合性较强,对复杂式子的变形能力要求较高。涉及直线与抛物线的位置关系,应用韦达定理,实现了整体代换,简化了解题过程。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
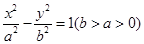 ,过右焦点
,过右焦点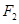 作双曲线的其中一条渐近线的垂线
作双曲线的其中一条渐近线的垂线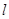 ,垂足为
,垂足为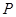 ,交另一条渐近线于
,交另一条渐近线于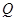 点,若
点,若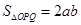 (其中
(其中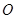 为坐标原点),则双曲线的离心率为( )
为坐标原点),则双曲线的离心率为( )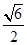
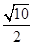
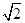
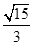
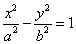 (
(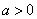 ,
,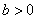 )的一条渐近线被圆
)的一条渐近线被圆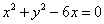 截得的弦长为
截得的弦长为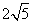 ,则双曲线的离心率为
,则双曲线的离心率为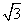
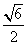

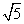
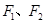 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为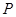 ,
,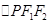 是以
是以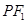 为底边的等腰三角形,若
为底边的等腰三角形,若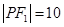 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为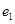 ,
,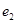 ,则
,则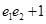 的取值范围是( )
的取值范围是( )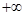 )
)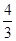 ,
,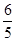 ,
,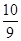 ,+
,+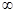 )
)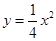 的焦点坐标是( )
的焦点坐标是( )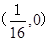
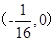
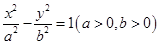 的左焦点
的左焦点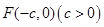 ,作倾斜角为
,作倾斜角为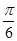 的直线FE交该双曲线右支于点P,若
的直线FE交该双曲线右支于点P,若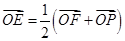 ,且
,且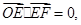 则双曲线的离心率为( )
则双曲线的离心率为( )
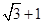

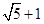
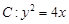 ,的焦点为F,直线
,的焦点为F,直线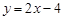 与抛物线C交于A、B两点,则
与抛物线C交于A、B两点,则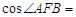 ( )
( )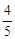
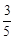


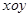 和极坐标系
和极坐标系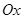 的原点与极点重合,
的原点与极点重合,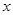 轴的正半轴与极轴重合,单位长度相同。已知曲线
轴的正半轴与极轴重合,单位长度相同。已知曲线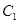 的极坐标方程为
的极坐标方程为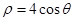 ,曲线
,曲线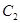 的参数方程为
的参数方程为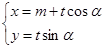
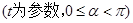 ,射线
,射线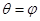 ,
,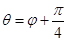 ,
,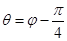 与曲线
与曲线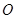 以外的三点A,B,C.
以外的三点A,B,C.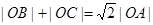 ;
;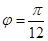 时,B,C两点在曲线
时,B,C两点在曲线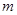 与
与 的值。
的值。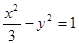 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为