题目内容
在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知曲线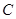 的参数方程为
的参数方程为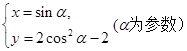 ,曲线
,曲线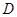 的极坐标方程为
的极坐标方程为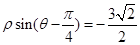 .
.
(Ⅰ)将曲线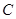 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)判断曲线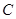 与曲线
与曲线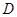 的交点个数,并说明理由.
的交点个数,并说明理由.
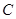 的参数方程为
的参数方程为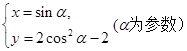 ,曲线
,曲线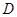 的极坐标方程为
的极坐标方程为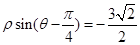 .
.(Ⅰ)将曲线
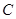 的参数方程化为普通方程;
的参数方程化为普通方程;(Ⅱ)判断曲线
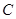 与曲线
与曲线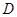 的交点个数,并说明理由.
的交点个数,并说明理由.(1)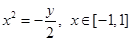 (2)曲线
(2)曲线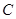 与曲线
与曲线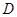 只有一个交点.
只有一个交点.
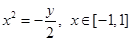 (2)曲线
(2)曲线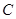 与曲线
与曲线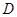 只有一个交点.
只有一个交点.试题分析:(Ⅰ)由已知得
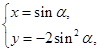 1分
1分消去参数
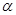 ,得
,得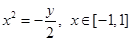 . 3分
. 3分(Ⅱ)由
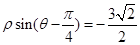 得曲线
得曲线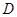 的直角坐标方程为
的直角坐标方程为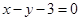 , 4分
, 4分由
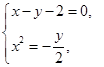 消去
消去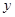 ,得
,得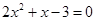 , 5分
, 5分解得
 6分
6分故曲线
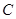 与曲线
与曲线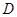 只有一个交点. 7分
只有一个交点. 7分点评:主要是考查了抛物线的参数方程以及直线的极坐标方程的运用,联立方程组求解交点的思想,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
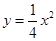 的焦点坐标是( )
的焦点坐标是( )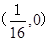
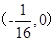
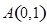 、
、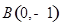 ,
, 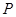 是一个动点, 且直线
是一个动点, 且直线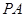 、
、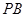 的斜率之积为
的斜率之积为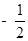 .
.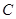 的方程;
的方程; 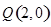 , 过点
, 过点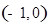 的直线
的直线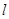 交
交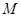 、
、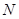 两点, 若对满足条件的任意直线
两点, 若对满足条件的任意直线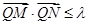 恒成立, 求
恒成立, 求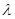 的最小值.
的最小值.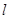 :
: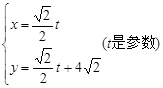 上的点向圆C:
上的点向圆C: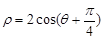 引切线,
引切线,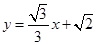 与圆心为D的圆
与圆心为D的圆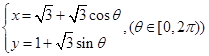 交于A、B两点,则直线AD与BD的倾斜角之和为( )
交于A、B两点,则直线AD与BD的倾斜角之和为( )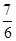 π
π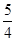 π
π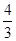 π
π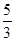 π
π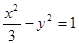 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为 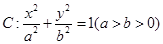 的离心率为
的离心率为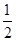 ,直线
,直线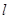 过点
过点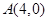 ,
,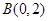 ,且与椭圆
,且与椭圆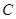 相切于点
相切于点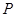 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆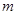 与椭圆
与椭圆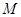 、
、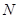 ,使得
,使得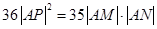 ?若存在,试求出直线
?若存在,试求出直线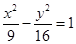 的一个焦点到一条渐近线的距离为______________
的一个焦点到一条渐近线的距离为______________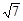 ,0),直线
,0),直线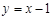 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为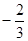 ,则此双曲线的方程是 .
,则此双曲线的方程是 .