题目内容
若抛物线顶点为坐标原点,对称轴为x轴,焦点在3x-4y-12=0上,那么抛物线方程是( )
A.y =16x =16x | B.y =-16x =-16x | C.y =12x =12x | D.y =-12x =-12x |
A
试题分析:根据题意,假设抛物线的标准方程,求得焦点坐标,代入3x-4y-12=0,从而可求抛物线的标准方程解:∵抛物线顶点为(0,0),对称轴为x轴,∴设抛物线方程为:y2=ax,∴焦点坐标为(
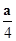 ,0),∵焦点在3x-4y-12=0上,∴3×
,0),∵焦点在3x-4y-12=0上,∴3×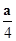 -12=0,∴a=16,∴抛物线的方程为y2=16x,故答案为A
-12=0,∴a=16,∴抛物线的方程为y2=16x,故答案为A点评:本题以抛物线的性质为依托,考查抛物线的标准方程,假设抛物线的标准方程是关键

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
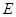 :
: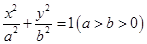 的一个焦点为
的一个焦点为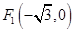 且过点
且过点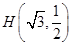 .
.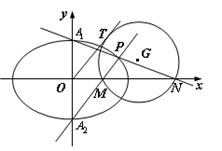
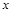 轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.
轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.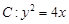 ,的焦点为F,直线
,的焦点为F,直线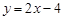 与抛物线C交于A、B两点,则
与抛物线C交于A、B两点,则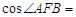 ( )
( )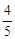
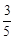


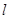 :
: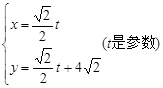 上的点向圆C:
上的点向圆C: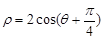 引切线,
引切线,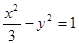 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为 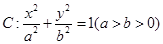 的离心率为
的离心率为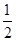 ,直线
,直线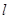 过点
过点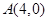 ,
,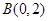 ,且与椭圆
,且与椭圆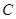 相切于点
相切于点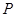 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆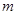 与椭圆
与椭圆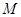 、
、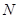 ,使得
,使得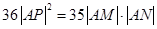 ?若存在,试求出直线
?若存在,试求出直线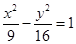 的一个焦点到一条渐近线的距离为______________
的一个焦点到一条渐近线的距离为______________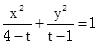 表示曲线
表示曲线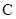 ,给出以下命题:
,给出以下命题: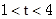 ,则曲线
,则曲线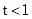 或
或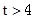 ;
;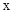 轴上的椭圆,则
轴上的椭圆,则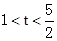 .
.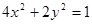 的一个焦点
的一个焦点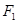 的直线与椭圆交于
的直线与椭圆交于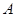 、
、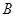 两点,则
两点,则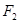 构成
构成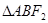 ,那么
,那么