题目内容
有两个人在一座11层大楼的底层进入电梯,设他们中的每一个人自第二层开始的每一层离开是等可能的,求两个人在不同层离开的概率.
两人中的第一个人自第二层开始在每一层离开是等可能的,即每人都可以从第二层到第十一层的任何一层离开,因此每人有10种离开的方法,所以共有不同的离开方法,即基本事件总数为n=10×10=100.
记“两个人在不同层离开”为事件A,下面求A包含的基本事件数.
第一人离开时有10种方法,第二人离开时有9种方法,故共有不同离开方法数是m=10×9=90.
∴由古典概型概率公式,得P(A)= =
=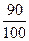 =0.9.
=0.9.
记“两个人在不同层离开”为事件A,下面求A包含的基本事件数.
第一人离开时有10种方法,第二人离开时有9种方法,故共有不同离开方法数是m=10×9=90.
∴由古典概型概率公式,得P(A)=
 =
=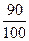 =0.9.
=0.9.由古典概型概率计算公式求解,两人离开的方法共有10×10=100种,两人在不同层离开有10×9=90种.

练习册系列答案
相关题目
 张卡片上分别写有数字
张卡片上分别写有数字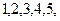 然后将它们混合,再任意排列成一行,则得到的数能被
然后将它们混合,再任意排列成一行,则得到的数能被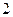 或
或

