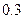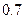题目内容
将编号为1,2，…，9的九个小球随机放置在圆周的九个等分点上，每个等分点上各有一个小球.设圆周上所有相邻两球号码之差的绝对值之和为要S.求使S达到最小值的放法的概率.（注：如果某种放法，经旋转或镜面反射后可与另一种放法重合，则认为是相同的放法）
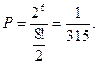
九个编号不同的小球放在圆周的九个等分点上，每点放一个，相当于九个不同元素在圆周上的一个圆形排列，故共有8！种放法，考虑到翻转因素，则本质不同的放法有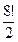
种.…5分
下求使S达到最小值的放法数：在圆周上，从1到9有优弧与劣弧两条路径，对其中任一条路径，设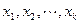
是依次排列于这段弧上的小球号码，则
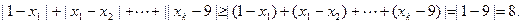上式取等号当且仅当
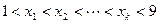，即每一弧段上的小球编号都是由1到9递增排列.
因此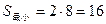
.…………………………………………………………………10分
由上知，当每个弧段上的球号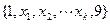
确定之后，达到最小值的排序方案便唯一确定.
在1,2，…，9中，除1与9外，剩下7个球号2,3，…，8，将它们分为两个子集，元素较少的一个子集共有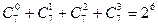
种情况，每种情况对应着圆周上使S值达到最小的唯一排法，即有利事件总数是
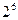种，故所求概率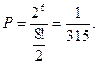……………20分
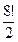种.…5分下求使S达到最小值的放法数：在圆周上，从1到9有优弧与劣弧两条路径，对其中任一条路径，设
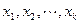是依次排列于这段弧上的小球号码，则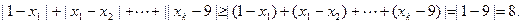上式取等号当且仅当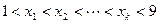，即每一弧段上的小球编号都是由1到9递增排列.因此
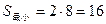.…………………………………………………………………10分由上知，当每个弧段上的球号
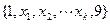确定之后，达到最小值的排序方案便唯一确定.在1,2，…，9中，除1与9外，剩下7个球号2,3，…，8，将它们分为两个子集，元素较少的一个子集共有
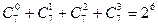种情况，每种情况对应着圆周上使S值达到最小的唯一排法，即有利事件总数是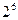种，故所求概率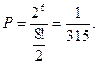……………20分
练习册系列答案
相关题目
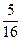
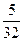
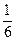
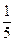
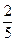
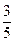
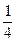
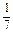.现有甲、乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有1人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
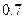，则恰有一人投中的概率是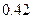
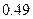
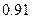
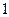个球，摸出红球的概率是
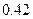，摸出白球的概率是
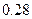，那么摸出黒球的概率是（ ）
