题目内容
同时抛掷两枚骰子.
(1)求“点数之和为6”的概率;
(2)求“至少有一个5点或6点”的概率.
(1)求“点数之和为6”的概率;
(2)求“至少有一个5点或6点”的概率.
(1)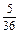 (2)
(2)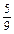
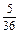 (2)
(2)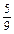
同时抛掷两枚骰子,可能的结果如下表:
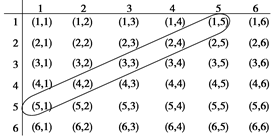
共有36个不同的结果. 7分
(1)点数之和为6的共有5个结果,所以点数之和为6的概率P=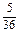 . 10分
. 10分
(2)方法一 从表中可以得其中至少有一个5点或6点的结果有20个,所以至少有一个5点或6点的概率
P=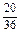 =
=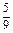 . 14分
. 14分
方法二 至少有一个5点或6点的对立事件是既没有5点又没有6点,如上表既没有5点又没有6点的结果共有16个,则既没有5点又没有6点的概率P=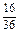 =
=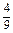 ,
,
所以至少有一个5点或6点的概率为1-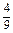 =
=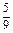 . 14分
. 14分

共有36个不同的结果. 7分
(1)点数之和为6的共有5个结果,所以点数之和为6的概率P=
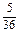 . 10分
. 10分(2)方法一 从表中可以得其中至少有一个5点或6点的结果有20个,所以至少有一个5点或6点的概率
P=
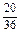 =
=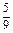 . 14分
. 14分方法二 至少有一个5点或6点的对立事件是既没有5点又没有6点,如上表既没有5点又没有6点的结果共有16个,则既没有5点又没有6点的概率P=
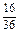 =
=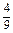 ,
,所以至少有一个5点或6点的概率为1-
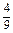 =
=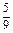 . 14分
. 14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
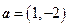 ,
,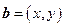 .
. 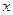 ,
, 分别表示将一枚质地均匀的正方体骰子(六个面
分别表示将一枚质地均匀的正方体骰子(六个面 的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足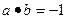 的
的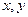
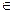
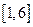 ,求满足
,求满足 的概率.
的概率.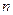 的球的重量为
的球的重量为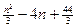 (克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.
(克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.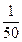
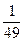
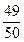
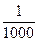
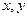 用
用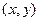 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中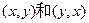 视为同一事件,并求
视为同一事件,并求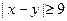 的事件A的概率。
的事件A的概率。