题目内容
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是: ,
,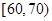 ,
,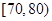 ,
,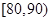 ,
, .
.
(1)求图中 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数( )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数( )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在 之外的人数.
之外的人数.
| 分数段 |  | 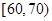 | 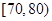 | 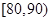 |
 |  |  |  | 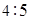 |
(1)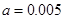 .(2)73.(3)10
.(2)73.(3)10
解析试题分析:(1)依题意得,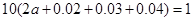 ,解得
,解得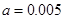 .
.
(2)这100名学生语文成绩的平均分为: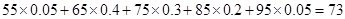 (分).
(分).
(3)数学成绩在 的人数为:
的人数为: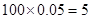 ,
,
数学成绩在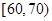 的人数为:
的人数为: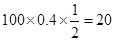 ,
,
数学成绩在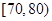 的人数为:
的人数为: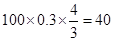 ,
,
数学成绩在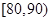 的人数为:
的人数为: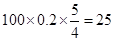 .
.
所以数学成绩在 之外的人数为:
之外的人数为: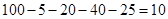 .
.
考点:本题考查了频率分布直方图的运用
点评:注意频率分布直方图中用小长方形面积的大小来表示在各个区间内取值的频率,所以在求频率时,通过已知求出所要区间的面积即可

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
某种产品的广告费支出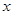 与销售额
与销售额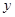 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
某校为了解高二学生 、
、 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试 、
、 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
| |  学科合格人数 学科合格人数 |  学科不合格人数 学科不合格人数 | 合计 |
 学科合格人数 学科合格人数 | 40 | 20 | 60 |
 学科不合格人数 学科不合格人数 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
 学科合格”与“
学科合格”与“ 学科合格”有关;
学科合格”有关;(2)从“
 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“ 学科合格”的人数为
学科合格”的人数为 ,求
,求 的数学期望.
的数学期望.附公式与表:

 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(理科)(本小题满分12分)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(文科)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.

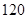 人,其中女性
人,其中女性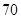 人,男性
人,男性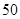 人.女性中有
人.女性中有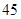 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外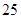 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外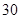 人主要的休闲方式是运动.
人主要的休闲方式是运动.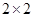 的列联表;
的列联表;
