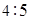题目内容
某种产品的广告费支出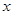 与销售额
与销售额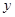 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
(1)正确画出散点图;
(2)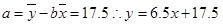 ;
;
(3)当x=10百万元时,y=92.5百万元。
解析试题分析:(1)正确画出散点图 3分
(2)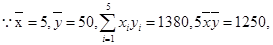
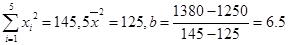
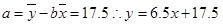
(3)当x=10百万元时,y=92.5百万元。 12分(写出回归方程给10分)
考点:本题主要考查散点图,回归直线方程的求法及其应用。
点评:中档题,确定回归直线方程,思路明确,关键是正确使用公式,细心计算。

练习册系列答案
相关题目
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
月份 | 1 | 2 | 3 | 4 | 5 |
用水量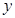 | 4 5 | 4 | 3 | 2 5 | 1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得
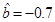 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是:
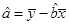 ,
,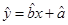
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 =bx+a;
=bx+a;(2)试预测加工10个零件需要多少时间?
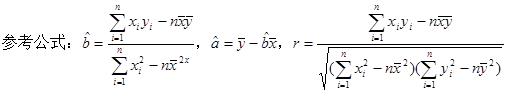
| n-2 | 1 | 2 | 3 | 4 |
| 小概率0.05 | 0.997 | 0.950 | 0.878 | 0.811 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 |
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了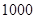 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.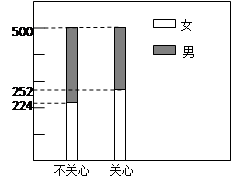
(1)完成列联表,并判断能否有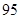 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
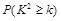 | 0.10 | 0.05 | 0.01 |
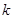 | 2.706 | 3.841 | 6.635 |
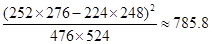
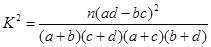 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望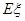 .
. 某糖厂为了了解一条自动生产线上袋装白糖的重量,随机抽取了100袋,并称出每袋白糖的重量(单位:g),得到如下频率分布表。
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 |  |
| [490.5,495.5) | 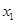 |  |
| [495.5,500.5) | 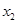 | 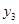 |
| [500.5,505.5] | 10 | |
| 合计 | 100 | |
 ,
, ,
,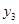 成等差数列。
成等差数列。(I)将有关数据分别填入所给的频率。分布表的所有空格内,并画出频率分布直方图。
(II)在这100包白糖的重量中,估计其中位数。
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(t)与相应的生产能耗y(t标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 ;
;(3)已知该厂技术改造前100t甲产品的生产能耗为90t标准煤,试根据(2)求出的线性回归方程预测生产100t甲产品的生产能耗比技术改造前降低多少吨标准煤?
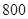 名男生中随机抽取
名男生中随机抽取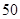 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于 cm和
cm和 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[ ),第二组[
),第二组[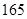 ),…,第八组[
),…,第八组[ ,
, 人.
人.
 cm以上(含
cm以上(含 ,事件
,事件 {
{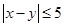 },事件
},事件 {
{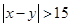 },求
},求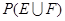 .
. ,
,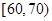 ,
,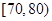 ,
,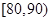 ,
, .
.
 的值;
的值; )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数( )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在 之外的人数.
之外的人数.