题目内容
已知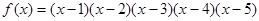 则
则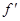
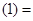
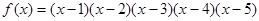 则
则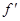
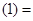
24
试题分析:根据题意,由于
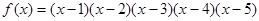 ,则根据导数的运算可知把第一个因式看做一个因式,后面的整体看做一个因式,则可知
,则根据导数的运算可知把第一个因式看做一个因式,后面的整体看做一个因式,则可知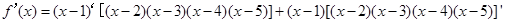 ,则可知
,则可知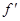
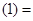
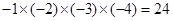 ,故答案为24.
,故答案为24.点评:解决的关键是对于多项式的理解和运算,整体思想的处理是关键,属于基础题。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
题目内容
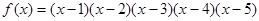 则
则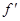
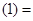
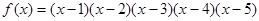 ,则根据导数的运算可知把第一个因式看做一个因式,后面的整体看做一个因式,则可知
,则根据导数的运算可知把第一个因式看做一个因式,后面的整体看做一个因式,则可知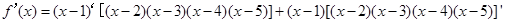 ,则可知
,则可知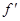
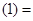
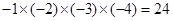 ,故答案为24.
,故答案为24.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案