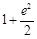题目内容
函数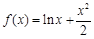 在区间
在区间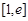 上的最大值是
上的最大值是
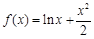 在区间
在区间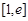 上的最大值是
上的最大值是 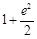
试题分析:根据题意,由于函数
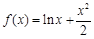 ,则其导数
,则其导数 恒成立,可知函数在给定区间
恒成立,可知函数在给定区间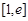 上单调递增,那么可知函数的最大值即为f(e)=
上单调递增,那么可知函数的最大值即为f(e)= 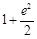 ,故答案为
,故答案为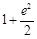
点评:解决的关键是利用导数的符号判定函数单调性,然后借助于单调性来求解最值。属于基础题。

练习册系列答案
相关题目
题目内容
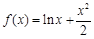 在区间
在区间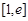 上的最大值是
上的最大值是 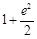
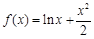 ,则其导数
,则其导数 恒成立,可知函数在给定区间
恒成立,可知函数在给定区间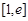 上单调递增,那么可知函数的最大值即为f(e)=
上单调递增,那么可知函数的最大值即为f(e)= 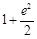 ,故答案为
,故答案为