题目内容
在R上定义运算“△”：x△y = x ( 2 – y )，若不等式( x + m )△x < 1对一切实数x恒成立，则实数m的取值范围是_______________．
【答案】
．
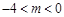【解析】解：由题意得：（x+m）△x=（x+m）（2-x）＜1，
变形整理得：x2+（m-2）x+（1-2m）＞0，
因为对任意的实数x不等式都成立，
所以其对应的一元二次方程：x2+（m-2）x+（1-2m）=0的根的判别式△=（m-2）2-4（1-2m）＜0，解得：-4＜m＜0．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
在R上定义运算⊙：x⊙y=x（1-y）．若不等式（x-a）⊙（x+a）＜1对任意实数x成立，则（ ）
| A、-1＜a＜1 | ||||
| B、0＜a＜2 | ||||
C、-
| ||||
D、-
|