题目内容
在R上定义运算⊙:x⊙y=x(1-y).若不等式(x-a)⊙(x+a)<1对任意实数x成立,则( )
| A、-1<a<1 | ||||
| B、0<a<2 | ||||
C、-
| ||||
D、-
|
分析:此题新定义运算⊙:x⊙y=x(1-y),由题意(x-a)⊙(x+a)=(x-a)(1-x-a),再根据(x-a)⊙(x+a)<1,列出不等式,然后把不等式解出来.
解答:解:∵(x-a)⊙(x+a)<1
∴(x-a)(1-x-a)<1,
即x2-x-a2+a+1>0
∵任意实数x成立,
故△=1-4(-a2+a+1)<0
∴-
<a<
,
故选C.
∴(x-a)(1-x-a)<1,
即x2-x-a2+a+1>0
∵任意实数x成立,
故△=1-4(-a2+a+1)<0
∴-
| 1 |
| 2 |
| 3 |
| 2 |
故选C.
点评:此题是一道新定义的题,要遵守命题人定的规则,另外此题主要还是考查一元二次不等式的解法.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 :x
:x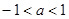 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.