题目内容
已知函数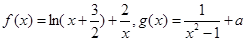
(1)求函数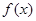 的单调区间.
的单调区间.
(2)若方程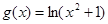 有4个不同的实根,求
有4个不同的实根,求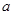 的范围?
的范围?
(3)是否存在正数 ,使得关于
,使得关于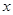 的方程
的方程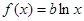 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由.
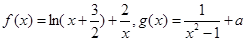
(1)求函数
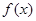 的单调区间.
的单调区间.(2)若方程
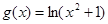 有4个不同的实根,求
有4个不同的实根,求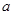 的范围?
的范围?(3)是否存在正数
 ,使得关于
,使得关于 的方程
的方程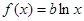 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由.(1)增区间为 ,减区间为
,减区间为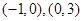 ;(2)
;(2)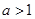 ;(3)不存在,理由见详解.
;(3)不存在,理由见详解.
 ,减区间为
,减区间为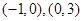 ;(2)
;(2)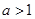 ;(3)不存在,理由见详解.
;(3)不存在,理由见详解.试题分析:(1)首先求导函数
 ,然后通过判断
,然后通过判断 的符号可求得单调区间;(2)构造函数
的符号可求得单调区间;(2)构造函数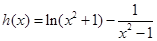 ,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函
,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函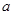 的取值范围;(3)
的取值范围;(3)试题解析:(1)根据
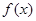 定义域后,求导得到
定义域后,求导得到 ,
,根据导数和0的关系得到在
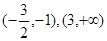 是函数
是函数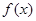 的增区间;在
的增区间;在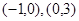 是函数
是函数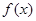 减区间.
减区间.(2)(2)令
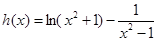 ,求导得
,求导得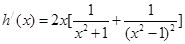 ,
,里面有一个零点
 和两个断点
和两个断点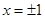 ,所以初步可以得到函数在区间
,所以初步可以得到函数在区间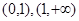 单调增;在区间
单调增;在区间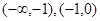 单调减.
单调减.当
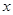 从负半轴方向趋近于-1时,
从负半轴方向趋近于-1时,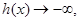
当
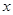 从正半轴方向趋近于-1时,
从正半轴方向趋近于-1时,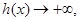
而且
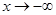 时,
时,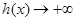 ,
,而且可以很容易得到
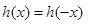 ,函数为偶函数,而且
,函数为偶函数,而且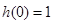 ,
,另半边的图像就容易模拟得到了,所以
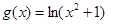 有4个不同的实根,结合图像得到
有4个不同的实根,结合图像得到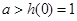 .
.(本题必须另半边如果不分析必须用奇偶性说明;而且必须说明在断点处的趋势,否则扣2到3分)
(3)结论:这样的正数
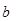 不存在.
不存在.假设存在满足条件的
 ,使得方程
,使得方程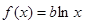 存在两个不相等的实根
存在两个不相等的实根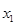 和
和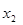 ,然后代入方程,根据其结构利用第(1)问的结论判断出
,然后代入方程,根据其结构利用第(1)问的结论判断出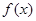 在
在 上的取值及单调性,然后结合假设导出矛盾,作出判断.
上的取值及单调性,然后结合假设导出矛盾,作出判断.假设存在正数
 ,使得方程
,使得方程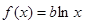 存在两个不相等的实根
存在两个不相等的实根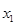 和
和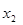 ,则
,则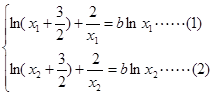
根据定义域知道
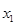 和
和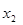 都是正数.
都是正数.根据第1问知道,当
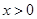 时,函数的最小值
时,函数的最小值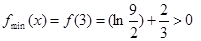 ,
,所以
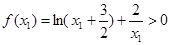 ,
,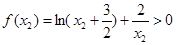
因为
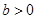 ,等式两边同号,所以,
,等式两边同号,所以,
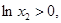 所以
所以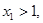
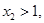
不妨设
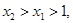
由(1)(2)可得
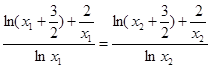 ,
,所以
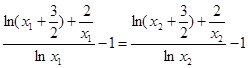 ,
,所以
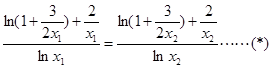 .
.因为很容易证明到函数
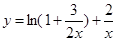 在
在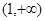 为恒大于0且为减函数
为恒大于0且为减函数所以(*)方程显然不成立,因为
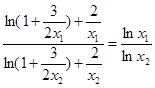 左边大于1,右边小于1.
左边大于1,右边小于1.所以原假设:存在正数
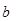 ,使得方程
,使得方程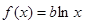 存在两个不相等的实根
存在两个不相等的实根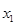 和
和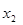 错误(本题其他证法,请酌情给分)
错误(本题其他证法,请酌情给分)
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
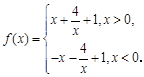
 的奇偶性;
的奇偶性; 和
和 上的增减性;
上的增减性;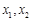 满足:
满足: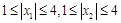 ,试证明:
,试证明: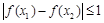 .
.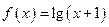 ,若
,若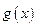 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当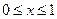 时,有
时,有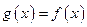 ,则函数
,则函数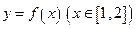 的反函数为( )
的反函数为( )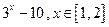
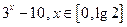


 ③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为.
③..y=f(x)的最小值为0,无最大值④.y=f(x)无最小值,最大值为sin1.正确的序号为. ,
,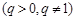 ;②
;② ;③
;③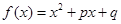 .
.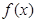 与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足
与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足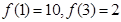 ,则
,则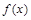 满足
满足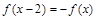 ,且在
,且在 上是增函数,则有( )
上是增函数,则有( )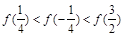
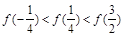
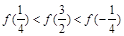
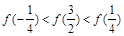
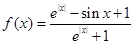 在
在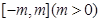 上的最大值为p,最小值为q,则p+q=
上的最大值为p,最小值为q,则p+q=  >0,给出下列命题:
>0,给出下列命题: )<f(x)的x的取值范围是( )
)<f(x)的x的取值范围是( )