题目内容
【题目】一种掷硬币走跳棋的游戏：在棋盘上标有第1站、第2站、第3站、…、第100站，共100站，设棋子跳到第
站的概率为
，一枚棋子开始在第1站，棋手每掷一次硬币，棋子向前跳动一次.若硬币的正面向上，棋子向前跳一站；若硬币的反面向上，棋子向前跳两站，直到棋子跳到第99站（失败）或者第100站（获胜）时，游戏结束.
（1）求
；
（2）求证：数列
为等比数列；
（3）求玩该游戏获胜的概率.
【答案】（1）
，
，
（2）证明见解析 （3）
【解析】
（1）根据题意，分析可得棋子在1站是一个必然事件，即可得P1的值，进而分析棋子跳到2站以及棋子跳到3站的情况，据此求出P2、P3的值（2）根据题意，分析可得
，变形可得
，即可得结论（3）由（2）知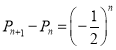
，利用累加法求出
，由对立事件的概率性质求出
.
（1）棋子开始在第1站是必然事件，
；
棋子跳到第2站，只有一种情况，第一次掷硬币正面向上，
其概率为
；
棋子跳到第3站，有两种情况，①第一次掷硬币反面向上，其概率为
；②前两次掷硬币都是正面向上，其概率为
；
（2）棋子棋子跳到第
站，有两种情况：①棋子先跳到第n站，又掷硬币反面向上，其概率为
；②棋子先跳到第
站，又掷硬币正面向上，其概率为
.故.
又
，
数列
…
是以
为首项，为公比的等比数列.
（3）由（2）得.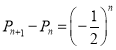
…
…
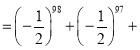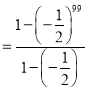
所以获胜的概率为
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量，某城市环保局随机抽取了一年内100天的空气质量指数（
）的检测数据，结果统计如下：
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
（1）从空气质量指数属于
，
的天数中任取3天，求这3天中空气质量至少有2天为优的概率；
（2）已知某企业每天的经济损失
（单位：元）与空气质量指数
的关系式为
，试估计该企业一个月（按30天计算）的经济损失的数学期望.
