Question

13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，点P（0，1）和点A（m，n）（m≠0）都在椭圆C上，直线PA交x轴于点M．
（Ⅰ）求椭圆C的方程，并求点M的坐标（用m，n表示）；
（Ⅱ）设O为原点，点B与点A关于x轴对称，直线PB交x轴于点N，问：y轴上是否存在点Q，使得∠OQM=∠ONQ？若存在，求点Q的坐标，若不存在，说明理由．

Answer 1

分析 （I）根据椭圆的几何性质得出$\left\{\begin{array}{l}{b=1}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$求解即可．
（II）求解得出M（$\frac{m}{1-n}$，0），N（$\frac{m}{1+n}$，0），运用图形得出tan∠OQM=tan∠ONQ，$\frac{{y}_{Q}}{{x}_{M}}$=$\frac{{x}_{Q}}{{y}_{Q}}$，求解即可得出即y_Q²=x_M•x_N，$\frac{{m}^{2}}{2}$+n²，根据m，m的关系整体求解．

解答 解：（Ⅰ）由题意得出$\left\{\begin{array}{l}{b=1}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$
解得：a=$\sqrt{2}$，b=1，c=1
∴$\frac{{x}^{2}}{2}$+y²=1，
∵P（0，1）和点A（m，n），-1＜n＜1
∴PA的方程为：y-1=$\frac{n-1}{m}$x，y=0时，x_M=$\frac{m}{1-n}$
∴M（$\frac{m}{1-n}$，0）
（II）∵点B与点A关于x轴对称，点A（m，n）（m≠0）
∴点B（m，-n）（m≠0）
∵直线PB交x轴于点N，
∴N（$\frac{m}{1+n}$，0），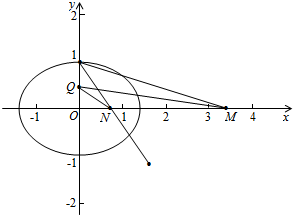

∵存在点Q，使得∠OQM=∠ONQ，Q（0，y_Q），
∴tan∠OQM=tan∠ONQ，
∴$\frac{{y}_{Q}}{{x}_{M}}$=$\frac{{x}_{N}}{{y}_{Q}}$，即y_Q²=x_M•x_N，$\frac{{m}^{2}}{2}$+n²=1
y_Q²=$\frac{{m}^{2}}{1-{n}^{2}}$=2，
∴y_Q=$±\sqrt{2}$，
故y轴上存在点Q，使得∠OQM=∠ONQ，Q（0，$\sqrt{2}$）或Q（0，-$\sqrt{2}$）

点评 本题考查了直线圆锥曲线的方程，位置关系，数形结合的思想的运用，运用代数的方法求解几何问题，难度较大，属于难题．