题目内容
已知数列 的前
的前 项和为
项和为 ,且
,且 .数列
.数列 为等比数列,且
为等比数列,且 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,且
,且 .数列
.数列 为等比数列,且
为等比数列,且 ,
, .
. (1)求数列
 ,
, 的通项公式;
的通项公式;(2)若数列
 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.(1) ,
, (2)
(2)
 ,
, (2)
(2)
试题分析:解:(Ⅰ )∵ 数列
 的前
的前 项和为
项和为 ,且
,且 ,
, ∴ 当
 时,
时, . 2分
. 2分当
 时,
时, 亦满足上式,
亦满足上式,故
 (
( ). 4分
). 4分又数列
 为等比数列,设公比为
为等比数列,设公比为 ,
, ∵
 ,
, , ∴
, ∴ . 6分
. 6分∴
 (
( ). 8分
). 8分(Ⅱ)
 . 10分
. 10分

 12分
12分 . 13分
. 13分所以
 . 14分
. 14分点评:解决的关键是利用等差数列和等比数列的通项公式来求解通项,同时能利用分组求和法来得到求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, ,则当
,则当 取得最小值时
取得最小值时 的值是 .
的值是 . 中,
中,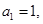 前
前 项和为
项和为 ,且点
,且点 在一次函数
在一次函数 的图象上,则
的图象上,则 =( )
=( )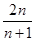
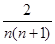


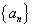 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).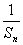 }是等差数列,并求公差;
}是等差数列,并求公差; 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 依次是等比数列
依次是等比数列 的前两项。
的前两项。
 且
且 ,使得数列
,使得数列 是常数列?若存在,求出
是常数列?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。 的前
的前 项和为
项和为 ,
, ,
, ,若
,若  ,则
,则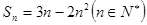 ,则当n>2时,下列不等式中的是( )
,则当n>2时,下列不等式中的是( )



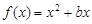 的图象在点
的图象在点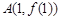 处的切线
处的切线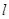 与直线
与直线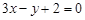 平行,若数
平行,若数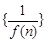 的前
的前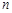 项和为
项和为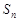 ,则
,则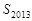 的值为 .
的值为 .