题目内容
5.在△ABC中,内角A,B,C的对边分别为a,b,c,且acosB=bcosA,a2+b2=c2+ab,则△ABC是( )| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
分析 由已知及正弦定理可得sinAcosB=sinBcosA,即sin(A-B)=0,结合A,B的范围,可得A=B,又a2+b2=c2+ab,由余弦定理可得cosC=$\frac{1}{2}$,解得C=$\frac{π}{3}$,从而可得A=B=C.
解答 解:∵acosB=bcosA,
∴由正弦定理可得:sinAcosB=sinBcosA,即得:sin(A-B)=0,
∵0<A<π,0<B<π,可得:-π<A-B<π,
∴解得:A-B=0,即A=B,
又∵a2+b2=c2+ab,由余弦定理可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,可解得:C=$\frac{π}{3}$,
∴可得:A=B=C,
故选:D.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
15.如图,在圆O中,弦AB的长是6,则$\overrightarrow{AO}$•$\overrightarrow{AB}$的值是( )
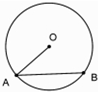

| A. | 18 | B. | -18 | C. | 36 | D. | 不能确定 |
20.在△ABC中,角B=60°,a=4$\sqrt{2},b=4\sqrt{3}$,那么角A=( )
| A. | 30° | B. | 45° | C. | 135° | D. | 45°或135° |
17.等差数列{an}的前n项和为sn,已知(a2-1)3+(a2-1)=sin$\frac{π}{3}$,(a2015-1)3+(a2015-1)=cos$\frac{5π}{6}$,则s2016=( )
| A. | 2015 | B. | 2016 | C. | $2015\sqrt{3}$ | D. | $2016\sqrt{3}$ |