题目内容
16.已知函数f(x)=2sinxsin($\frac{π}{2}$+x).(1)求f(x)的最小正周期;
(2)求f(x)在区间[-$\frac{π}{6}$,$\frac{π}{2}$]上的最大值和最小值.
分析 (1)利用诱导公式、二倍角公式求得函数f(x)=sin2x,再利用正弦函数的周期性,求得f(x)的最小正周期.
(2)由x∈[-$\frac{π}{6}$,$\frac{π}{2}$],利用正弦函数的定义域和值域,求得f(x)在区间[-$\frac{π}{6}$,$\frac{π}{2}$]上的最大值和最小值.
解答 解:(1)函数f(x)=2sinxsin($\frac{π}{2}$+x)=2sinxcosx=sin2x,∴f(x)的最小正周期为$\frac{2π}{2}$=π.
(2)由x∈[-$\frac{π}{6}$,$\frac{π}{2}$],可得当2x∈[-$\frac{π}{3}$,π],∴当2x=$\frac{π}{3}$时,函数f(x)取得最小值为-$\frac{\sqrt{3}}{2}$;
当2x=$\frac{π}{2}$时,函数f(x)取得最大值为1.
点评 本题主要考查二倍角公式,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
4.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,-2),则与向量$\overrightarrow{b}$-$\overrightarrow{a}$垂直的单位向量为( )
| A. | (-2,1)或(2,-1) | B. | (-1,2)或(1,-2) | ||
| C. | (-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$)或($\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$) | D. | (-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) |
11.函数y=lg(x-10)的定义域为( )
| A. | {x|x<1} | B. | {x|x>10} | C. | {x|0<x<10} | D. | {x|x≥10} |
1.已知“x<k”是“x2>4”的充分不必要条件,则实数k的取值范围是( )
| A. | (-∞,-2] | B. | (-∞,-2) | C. | (2,+∞) | D. | [-2,2) |
5.在△ABC中,内角A,B,C的对边分别为a,b,c,且acosB=bcosA,a2+b2=c2+ab,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
6.已知f(x)=1+x-sinx,则f(2),f(3),f(π)的大小关系正确的是( )
| A. | f(2)>f(3)>f(π) | B. | f(3)>f(2)>f(π) | C. | f(2)>f(π)>f(3) | D. | f(π)>f(3)>f(2) |
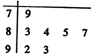 七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.
七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.