题目内容
15.如图,在圆O中,弦AB的长是6,则$\overrightarrow{AO}$•$\overrightarrow{AB}$的值是( )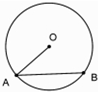
| A. | 18 | B. | -18 | C. | 36 | D. | 不能确定 |
分析 如图所示,过点O作OD⊥AB,垂足为D,利用垂经定理可得AD=DB.于是$\overrightarrow{AO}$•$\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$,即可得出.
解答 解:如图所示,过点O作OD⊥AB,垂足为D,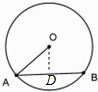
则AD=DB.
∴$\overrightarrow{AO}$•$\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=$\frac{1}{2}×{6}^{2}$=18.
故选:A.
点评 本题考查了垂经定理、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
10.函数f(x)=sinx-2cosx=$\sqrt{5}$sin(x+φ),则cosφ等于( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
4.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,-2),则与向量$\overrightarrow{b}$-$\overrightarrow{a}$垂直的单位向量为( )
| A. | (-2,1)或(2,-1) | B. | (-1,2)或(1,-2) | ||
| C. | (-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$)或($\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$) | D. | (-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) |
5.在△ABC中,内角A,B,C的对边分别为a,b,c,且acosB=bcosA,a2+b2=c2+ab,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
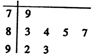 七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.
七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.