题目内容
17.等差数列{an}的前n项和为sn,已知(a2-1)3+(a2-1)=sin$\frac{π}{3}$,(a2015-1)3+(a2015-1)=cos$\frac{5π}{6}$,则s2016=( )| A. | 2015 | B. | 2016 | C. | $2015\sqrt{3}$ | D. | $2016\sqrt{3}$ |
分析 已知两个等式相加因式分解即可得到a2+a2015的值,利用等差数列的性质及数列的前n项和公式可得.
解答 解:∵(a2-1)3+(a2-1)=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$ ①
(a2015-1)3+(a2015-1)=cos$\frac{5π}{6}$=-$\frac{\sqrt{3}}{2}$ ②
①+②得(a2-1)3+(a2-1)+(a2015-1)3+(a2015-1)=0,
即(a2-1+a2015-1)[(a2-1)2-(a2-1)((a2015-1)+(a2015-1)2]+(a2-1+a2015-1)=0,
∴a2-1+a2015-1=0,即a2+a2015=2,
∴S2016=$\frac{2016({a}_{1}+{a}_{2016})}{2}$=1008(a2+a2015)=1008×2=2016,
故选:B.
点评 本题考查等差数列的前n项和,根据条件求出a2+a2015=2是解决本题的关键,属中档题.

练习册系列答案
相关题目
5.在△ABC中,内角A,B,C的对边分别为a,b,c,且acosB=bcosA,a2+b2=c2+ab,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
12.在复平面内,复数$\frac{3-2i}{{{i^{\;}}}}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第三四象限 |
2.集合M={x|1<x+1≤3},N={x|x2-2x-3>0},则(∁RM)∩(∁RN)等于( )
| A. | (-1,3) | B. | (-1,0)∪(2,3) | C. | (-1,0]∪[2,3) | D. | [-1,0]∪(2,3] |
6.已知f(x)=1+x-sinx,则f(2),f(3),f(π)的大小关系正确的是( )
| A. | f(2)>f(3)>f(π) | B. | f(3)>f(2)>f(π) | C. | f(2)>f(π)>f(3) | D. | f(π)>f(3)>f(2) |
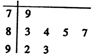 七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.
七位评委为某跳水运动员打出的分数的茎叶图如图,其极差为14.