题目内容
(本小题满分14分)已知函数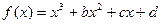 在(0,+
在(0,+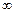 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程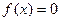 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.
(1)求c的值;(2)求证: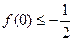 ;(3)求|α–β|的取值范围.
;(3)求|α–β|的取值范围.
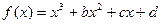 在(0,+
在(0,+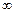 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程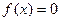 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.(1)求c的值;(2)求证:
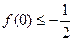 ;(3)求|α–β|的取值范围.
;(3)求|α–β|的取值范围.(Ⅰ) 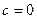 (Ⅱ) b≥
(Ⅱ) b≥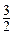 (Ⅲ)
(Ⅲ)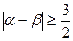
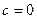 (Ⅱ) b≥
(Ⅱ) b≥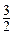 (Ⅲ)
(Ⅲ)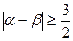
(1)解: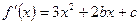 由题意知:函数
由题意知:函数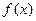 在(0,+
在(0,+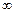 )上是增函数,在[–1,0]上是减函数,函数
)上是增函数,在[–1,0]上是减函数,函数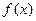 在x=0处有极小值,∴
在x=0处有极小值,∴ 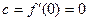
(2)证明:∵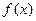 在(0,+
在(0,+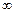 )上是增函数,在[–1,0]上是减函数,∴
)上是增函数,在[–1,0]上是减函数,∴ 在(0,+
在(0,+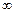 )
)
上恒成立,且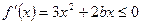 在
在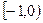 上恒成立,即
上恒成立,即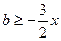 在(0,+
在(0,+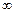 )上恒成立, 在
)上恒成立, 在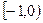 上也恒成立,∴ b≥
上也恒成立,∴ b≥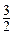 .又∵
.又∵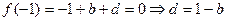 ,∴
,∴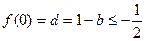 即
即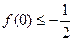 .
.
(3)解:∵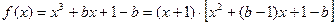 ,∴ α,β是方程
,∴ α,β是方程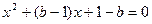 的两根,∴ 当
的两根,∴ 当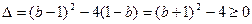
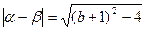 又 b≥
又 b≥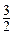 , 所以
, 所以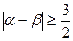 .
.
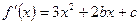 由题意知:函数
由题意知:函数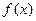 在(0,+
在(0,+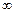 )上是增函数,在[–1,0]上是减函数,函数
)上是增函数,在[–1,0]上是减函数,函数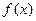 在x=0处有极小值,∴
在x=0处有极小值,∴ 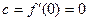
(2)证明:∵
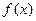 在(0,+
在(0,+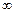 )上是增函数,在[–1,0]上是减函数,∴
)上是增函数,在[–1,0]上是减函数,∴ 在(0,+
在(0,+ )
)上恒成立,且
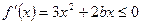 在
在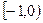 上恒成立,即
上恒成立,即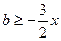 在(0,+
在(0,+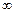 )上恒成立, 在
)上恒成立, 在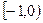 上也恒成立,∴ b≥
上也恒成立,∴ b≥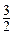 .又∵
.又∵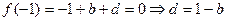 ,∴
,∴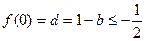 即
即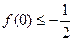 .
.(3)解:∵
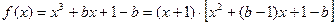 ,∴ α,β是方程
,∴ α,β是方程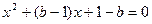 的两根,∴ 当
的两根,∴ 当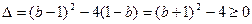
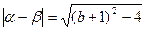 又 b≥
又 b≥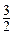 , 所以
, 所以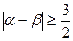 .
.
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )(1)求
)(1)求 ,求证:当
,求证:当 时,
时, ;(3)是否存在实数a,使得当
;(3)是否存在实数a,使得当 时,
时,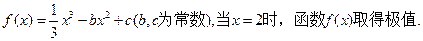
 的单调区间;(Ⅱ)若函数
的单调区间;(Ⅱ)若函数
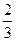 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R).  ,若
,若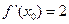 ,则
,则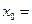 ( )
( )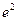


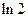
 ,若,
,若,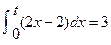 ,则
,则 。
。