题目内容
【题目】如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F. 
(1)求证:ACBC=ADAE;
(2)若AF=2,CF=2 ![]() ,求AE的长.
,求AE的长.
【答案】
(1)证明:如图所示,连接BE.
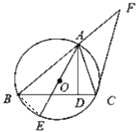
∵AE是⊙O的直径,∴∠ABE=90°.
又∠E与∠ACB都是 ![]() 所对的圆周角,
所对的圆周角,
∴∠E=∠ACB.
∵AD⊥BC,∠ADC=90°.
∴△ABE∽△ADC,
∴AB:AD=AE:AC,
∴ABAC=ADAE.
又AB=BC,
∴BCAC=ADAE.
(2)解:∵CF是⊙O的切线,
∴CF2=AFBF,
∵AF=2,CF=2 ![]() ,
,
∴(2 ![]() )2=2BF,解得BF=4.
)2=2BF,解得BF=4.
∴AB=BF﹣AF=2.
∵∠ACF=∠FBC,∠CFB=∠AFC,
∴△AFC∽△CFB,
∴AF:FC=AC:BC,
∴AC= ![]() =
= ![]() .
.
∴cos∠ACD= ![]() ,
,
∴sin∠ACD= ![]() =sin∠AEB,
=sin∠AEB,
∴AE= ![]() =
= ![]()
【解析】(1)如图所示,连接BE.由于AE是⊙O的直径,可得∠ABE=90°.利用∠E与∠ACB都是 ![]() 所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(2)利用切割线定理可得CF2=AFBF,可得BF.再利用△AFC∽△CFB,可得AF:FC=AC:BC,进而根据sin∠ACD=sin∠AEB,AE=
所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.(2)利用切割线定理可得CF2=AFBF,可得BF.再利用△AFC∽△CFB,可得AF:FC=AC:BC,进而根据sin∠ACD=sin∠AEB,AE= ![]() ,即可得出答案.
,即可得出答案.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了很大的便利,但也给城市的管理带来了一些困难,现某城市为了解人们对“共享单车”投放的认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 赞成投放的人数 | 赞成投放的人数占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|
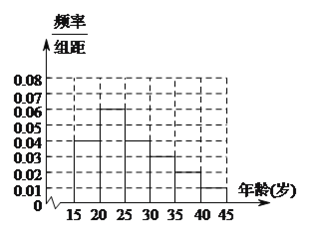
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取
)在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取![]() 人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
(![]() )在(
)在(![]() )中抽取的
)中抽取的![]() 人中随机选派
人中随机选派![]() 人作为领队,求所选派的
人作为领队,求所选派的![]() 人中第五组至少有一人的概率.
人中第五组至少有一人的概率.
【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
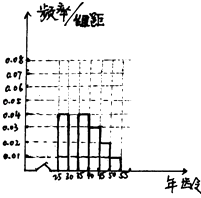
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.