题目内容
已知(
-
)n(n∈N*)展开式中二项式系数和为256.
(1)此展开式中有没有常数项?有理项的个数是几个?并说明理由.
(2)求展开式中系数最小的项.
| x |
| 2 |
| x2 |
(1)此展开式中有没有常数项?有理项的个数是几个?并说明理由.
(2)求展开式中系数最小的项.
(1)由题意,二项式系数和为2n=256,解得n=8,
通项Tr+1=
(
)8-r•(-
)r=
(-2)rx
,
若Tr+1为常数项,当且仅当
=0,即5r=8,且r∈Z,这是不可能的,
∴展开式中不含常数项.
若Tr+1为有理项,当且仅当
∈Z,且0≤r≤8,即r=0,2,4,6,8,
∴展开式中共有5个有理项;
(2)设展开式中第r项,第r+1项,第r+2项的系数绝对值分别为
•2r-1,
•2r,
•
,
若第r+1项的系数绝对值最大,则
,解得5≤r≤6,
又∵r∈Z,
∴r=5或6.
∵r=5时,第6项的系数为负,r=6时,第7项的系数为正,
∴系数最小的项为T6=
(-2)5x-
=-1792•x-
.
通项Tr+1=
| C | r8 |
| x |
| 2 |
| x2 |
| C | r8 |
| 8-5r |
| 2 |
若Tr+1为常数项,当且仅当
| 8-5r |
| 2 |
∴展开式中不含常数项.
若Tr+1为有理项,当且仅当
| 8-5r |
| 2 |
∴展开式中共有5个有理项;
(2)设展开式中第r项,第r+1项,第r+2项的系数绝对值分别为
| C | r-18 |
| C | r8 |
| C | r+18 |
| 2 | r+1 |
若第r+1项的系数绝对值最大,则
|
又∵r∈Z,
∴r=5或6.
∵r=5时,第6项的系数为负,r=6时,第7项的系数为正,
∴系数最小的项为T6=
| C | 58 |
| 17 |
| 2 |
| 17 |
| 2 |

练习册系列答案
相关题目
 月
月



 销售商支付给果园的费用
销售商支付给果园的费用 运费)
运费) (单位:万元),求
(单位:万元),求 ;
; ,求
,求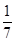 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.