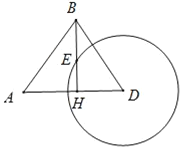
题目内容
【题目】 已知抛物线![]() 的顶点为坐标原点
的顶点为坐标原点![]() ,焦点
,焦点![]() 在
在![]() 轴的正半轴上,过点
轴的正半轴上,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() ,
,![]() 两点,且满足
两点,且满足![]()
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 是抛物线
是抛物线![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2) 8
(2) 8
【解析】
(1)设直线![]() 的方程为
的方程为![]() 由直线方程与抛物线方程联立,消元后可
由直线方程与抛物线方程联立,消元后可![]() ,代入
,代入![]() 可求得
可求得![]() ,得抛物线方程;
,得抛物线方程;
(2)设![]() 易知点M,N的横坐标与P的横坐标均不相同.不妨设m
易知点M,N的横坐标与P的横坐标均不相同.不妨设m![]() n. 写出直线PM的方程,由直线PM与圆相切得一关系式,同理PN与圆相切又得一关系式,两者比较说明
n. 写出直线PM的方程,由直线PM与圆相切得一关系式,同理PN与圆相切又得一关系式,两者比较说明![]() 是一个方程的根,由韦达定理得
是一个方程的根,由韦达定理得![]() ,从而可表示并求出
,从而可表示并求出![]() (用
(用![]() 表示),而
表示),而![]() 面积为
面积为![]() ,表示为
,表示为![]() 的函数,由基本不等式可求得最小值.
的函数,由基本不等式可求得最小值.
(1)由题意,设抛物线C的方程为![]() ,则焦点F的坐标为
,则焦点F的坐标为![]() .
.
设直线![]() 的方程为
的方程为![]()
联立方程得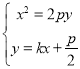 ,消去
,消去![]() 得
得![]()
所以![]()
因为![]() 所以
所以![]() 故抛物线的方程为
故抛物线的方程为![]() .
.
(2)设![]() 易知点M,N的横坐标与P的横坐标均不相同.
易知点M,N的横坐标与P的横坐标均不相同.
不妨设m![]() n.
n.
易得直线PM的方程为![]() 化简得
化简得![]() ,
,
又圆心(0,1)到直线PM的距离为1,所以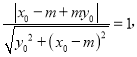
所以![]()
不难发现![]() ,故上式可化为
,故上式可化为![]()
同理可得![]()
所以m,n可以看作是![]() 的两个实数根,则
的两个实数根,则
![]() 所以
所以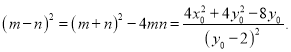
因为![]() 是抛物线C上的点,所以
是抛物线C上的点,所以![]()
则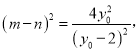 又
又![]() ,所以
,所以![]() 从而
从而
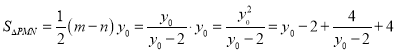
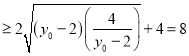
当且仅当![]() 时取得等号,此时
时取得等号,此时![]()
故△PMN面积的最小值为8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目