Question

【题目】已知函数f（x）＝lnx+ax2+ax．

（1）若曲线y＝f（x）在点P（1，f（1））处的切线与直线y＝4x+1平行，求实数a的值；

（2）若时，关于x的方程在（0，2]上恰有两个不相等的实数根，求实数b的取值范围．

Answer 1

【答案】（1）a＝1．（2）[ln2﹣5，）．

【解析】

（1）求导后，进行求解；（2）分离参数通过画出新函数图象，根据直线和函数图象有两个交点求出实数b的取值范围.

（1）由题意，f′（x）2ax+a，x＞0．

根据题意，有f′（1）＝3a+1＝4，

解得a＝1．

（2）由题意，f（x）＝lnxx2x，

则lnxx2xx+b，

即b＝lnxx2x，

令g（x）＝lnxx2x，x＞0．则

g′（x）x．

令g′（x）＝0，解得x＝1，或x＝2；

令g′（x）＞0，解得0＜x＜1，或x＞2；

令g′（x）＜0，解得1＜x＜2．

∴函数g（x）在（0，1）上单调递增，在（1，2）上单调递减，

在x＝1处取得极大值g（1），

在x＝2处取得极小值g（2）＝ln2﹣5．

故函数g（x）在（0，2]上大致图象如下：

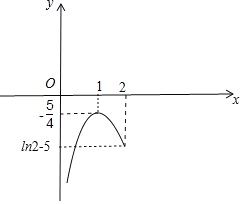
根据题意及图，可知

实数b的取值范围为：[ln2﹣5，）．