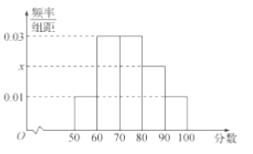
题目内容
【题目】已知定义在R上的函数f（x）是满足f（x）+f（﹣x）=0，在（﹣∞，0）上 
，且f（5）=0，则使f（x）＜0的x取值范围是
【答案】【分析】由条件及奇函数、减函数的定义便知f（x）为奇函数，且在（﹣∞，0），（0，+∞）上为减函数，且有f（﹣5）=f（5）=0，从而可分别讨论x＞0，和x＜0从而得出 
，或 
，这样根据f（x）的单调性即可得出x的取值范围．
【解析】解：根据条件知，f（x）在R上为奇函数，在（﹣∞，0）上单调递减；
∴f（x）在（0，+∞）上单调递减，且f（﹣5）=f（5）=0；
∴①x＞0时，由f（x）＜0得，f（x）＜f（5）；
∴x＞5；
②x＜0时，由f（x）＜0得，f（x）＜f（﹣5）；
﹣5＜x＜0；
∴x的取值范围为（﹣5，0）∪（5，+∞）．
所以答案是：（﹣5，0）∪（5，+∞）．
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识，掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．
练习册系列答案
相关题目
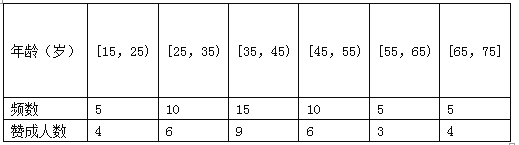
【题目】某学校高一 、高二 、高三三个年级共有 
名教师，为调查他们的备课时间情况，通过分层
抽样获得了
名教师一周的备课时间 ，数据如下表（单位 ：小时）：
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
（1）试估计该校高三年级的教师人数 ；
（2）从高一年级和高二年级抽出的教师中，各随机选取一人，高一年级选出的人记为甲 ，高二年级选出的人记为乙 ，求该周甲的备课时间不比乙的备课时间长的概率 ；
（3）再从高一、高二、高三三个年级中各随机抽取一名教师，他们该周的备课时间分别是
（单位： 小时），这三个数据与表格中的数据构成的新样本的平均数记为
，表格中的数据平均数记为
，试判断
与
的大小. （结论不要求证明）
