Question

8．如图，在多面体ABCDEF中，四边形ABCD为菱形，∠ABC=60°，EC⊥面ABCD，FA⊥面ABCD，G为BF的中点，若EG⊥面ABF，AB=2．
（1）求证：EG∥面ABCD；
（2）若AF=AB，求二面角B-EF-D的余弦值．

Answer 1

分析 （1）方法一：根据线面平行的判定定理即可证明EG∥面ABCD；
方法二：建立坐标系，利用向量法进行证明．
（2）方法一：根据二面角的定义求出二面角的平面角，根据边角关系进行求解即可．
方法二：求出平面的法向量，利用向量法即可，求二面角B-EF-D的余弦值．

解答 解：解法一（（1）不建系）：
（1）（解法一）取AB的中点M，连结GM，MC，G为BF的中点，∴GM∥FA，…（1分）
又EC⊥面ABCD，FA⊥面ABCD，
∴CE∥AF，…（2分）
∴CE∥GM，且GM⊥面ABCD，…（3分）
∴四边形CEGM为平面四边形．…（4分）
又因为MC?面ABCD，
∴GM⊥MC，…（5分）
∵EG⊥面ABCD，
又∵GM?面ABF，
∴GE⊥MG，∴EG∥CM，…（6分）
又因为MC?面ABCD，EG?面ABCD，
∴EG∥面ABCD  …（7分）
（解法二）∵ABCD为菱形，∠ABC=60°，∴△ABC为正三角形，…（1分）
又∵M是AB的中点，∴MC⊥AB，…（2分）
又∵FA⊥面ABCD，MC?面ABCD，∴FA⊥MC，…（3分）
AB∩FA=A，∴MC⊥面ABF，…（4分）
已知EG⊥面ABF，∴MC∥EG   …（5分）
又因为MC?面ABCD，EG?面ABCD，
∴EG∥面ABCD  …（7分）
（2）（解法一）由题意知△FAB≌△FAD，∴FB=FD=2$\sqrt{2}$…（1分）
同理△FAB≌△FAD，EB=ED=$\sqrt{5}$，…（2分），
∴△FEB≌△FED，…（3分），
过B作BH⊥FE，连HD，则DH⊥FE，…（4分），∴∠BHD为所求角的平面角…（5分），
在直角梯形FACE中，FE=$\sqrt{5}$，
根据面积相等FB•EG=BH•FE得$BH=\frac{{2\sqrt{30}}}{5}$…（6分），
在△BHD中，根据余弦定理得COS∠BHD=$-\frac{1}{4}$，
∴为所求角的余弦值为$-\frac{1}{4}$ …（7分）
（解法二）建立如图所示的坐标系，∵AB=2，AF=AB，由（1）知四边形GMCE为矩形．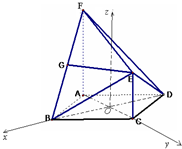
则B（$\sqrt{3}，0，0$）E（0，1，1）F（0，-1，2）$\overrightarrow{EF}$=（0，-2，1），$\overrightarrow{EB}$=（$\sqrt{3}$，-1，-1），$\overrightarrow{DE}$=（$\sqrt{3}$，1，1），…（10分）
设平面BEF的法向量n₁=（x，y，z）
则$\left\{\begin{array}{l}-2y+z=0\\ \sqrt{3}x-y-z=0\end{array}\right.$令y=1，则$z=2，x=\sqrt{3}$，
∴n₁=（$\sqrt{3}，1，2$）…（12分）
同理，可求平面DEF的法向量  n₂=（-$\sqrt{3}，1，2$）…（13分）
设所求二面角的平面角为θ，则  cosθ=$-\frac{1}{4}$．…（14分）
解法二（（1）、（2）均建系）：
（1）建立如图所示的坐标系，因为AB=2，设AF=b，则A（0，-1，0），B（$\sqrt{3}，0，0$），F（0，-1，b），G（$\frac{{\sqrt{3}}}{2}，-\frac{1}{2}，\frac{b}{2}$），E（0，1，c）  …（3分）
∵EG⊥面ABF，∴EG⊥AB，EG⊥AF，…（4分）
∴$\left\{{\begin{array}{l}{\overrightarrow{EG}•\overrightarrow{FB}=0}\\{\overrightarrow{EG}•\overrightarrow{AF}=0}\end{array}}\right.$…（5分）
∴$\left\{{\begin{array}{l}{（\frac{{\sqrt{3}}}{2}，-\frac{3}{2}，\frac{b}{2}-c）•（\sqrt{3}，1，-b）=0}\\{（\frac{{\sqrt{3}}}{2}，-\frac{3}{2}，\frac{b}{2}-c）•（0，0，b）=0}\end{array}}\right.$解得b=2c．…（7分）
∴$\overrightarrow{EG}=（\frac{{\sqrt{3}}}{2}，-\frac{3}{2}，0）$，∴$\overrightarrow{EG}•\overrightarrow{AF}=0$，…（8分）
由已知FA⊥面ABCD，EG?平面ABCD上，
∴EG∥平面ABCD     …（9分）
（2）∵AF=AB，则E（0，1，1）F（0，-1，2）
$\overrightarrow{EF}$=（0，-2，1），$\overrightarrow{EB}$=（$\sqrt{3}$，-1，-1），$\overrightarrow{DE}$=（$\sqrt{3}$，1，1），…（10分）
设平面BEF的法向量$\overrightarrow{{n}_{1}}$=（x，y，z）则
$\left\{\begin{array}{l}{-2y+z=0}\\{\sqrt{3}x-y-z=0}\end{array}\right.$，
令y=1，则z=2，x=$\sqrt{3}$，…（11分）
∴$\overrightarrow{{n}_{1}}$=（$\sqrt{3}$，1，2）…（12分）
同理，可求平面DEF的法向量$\overrightarrow{{n}_{2}}$=（-$\sqrt{3}$，1，2）…（13分）
设所求二面角的平面角为θ，
则cos$θ=-\frac{1}{4}$…（14分）

点评 本题主要考查线面平行的判定，以及空间二面角的求解，根据定义法以及向量法是解决本题的关键．