题目内容
(本小题满分14分)
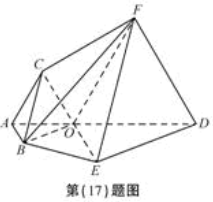
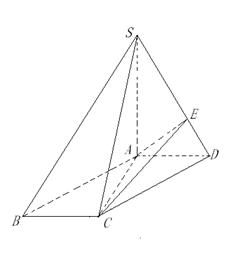
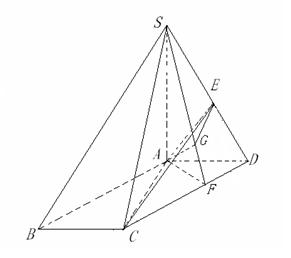
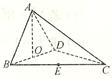
如图,在四棱锥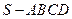 中,底面
中,底面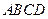 为平行四边形,
为平行四边形,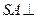 平面
平面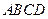 ,
,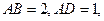
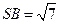
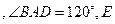 在棱
在棱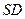 上
上 .
.
(Ⅰ)当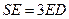 时,求证
时,求证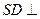 平面
平面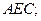
(Ⅱ)当二面角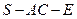 的大小为
的大小为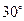 时,求直线
时,求直线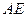 与平面
与平面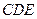 所成角的正弦值.
所成角的正弦值.
如图,在四棱锥
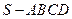 中,底面
中,底面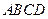 为平行四边形,
为平行四边形,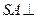 平面
平面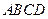 ,
,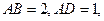
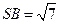
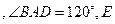 在棱
在棱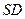 上
上 .
.
(Ⅰ)当
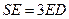 时,求证
时,求证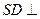 平面
平面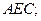
(Ⅱ)当二面角
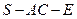 的大小为
的大小为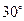 时,求直线
时,求直线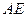 与平面
与平面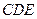 所成角的正弦值.
所成角的正弦值.解:(Ⅰ)在平行四边形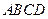 中,由
中,由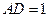 ,
, ,
,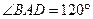 ,
,
易知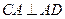 ,…………………2分
,…………………2分
又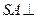 平面
平面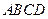 ,所以
,所以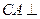 平面
平面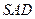 ,
,
∴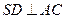 ,
,
在直角三角形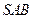 中,易得
中,易得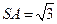 ,
,
在直角三角形
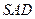 中,
中,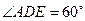 ,
,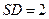 ,
,
又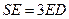 ,∴
,∴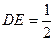 ,
,
可得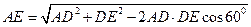
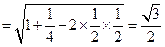 .
.
∴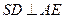 ,
, ……………………6
……………………6 分
分
又∵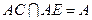 ,∴
,∴
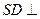 平面
平面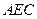 .………7分
.………7分
(Ⅱ)由(Ⅰ)可知,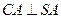 ,
,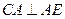 ,
,
可知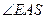 为二面角
为二面角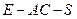 的平面角,
的平面角,
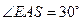 ,此时
,此时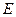 为
为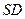 的中点. ……………9分
的中点. ……………9分
过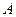 作
作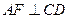
 ,连结
,连结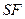 ,则平面
,则平面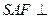 平面
平面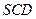 ,
,
作
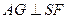 ,则
,则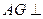 平面
平面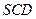 ,连结
,连结
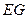 ,
,
可得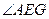 为直线
为直线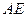 与平面
与平面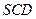 所成的角.
所成的角.
因为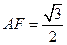 ,
,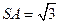 ,
,
所以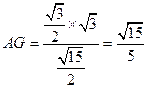 .……
.…… ………12分
………12分
在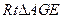 中,
中,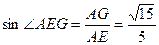
直线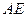 与平面
与平面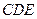 所成角的正弦值大小为
所成角的正弦值大小为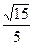 .……………………14分
.……………………14分
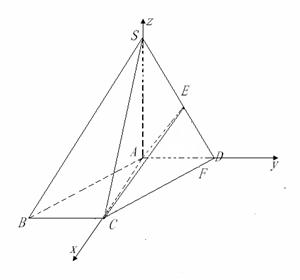
解法二:依题意易知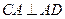 ,
,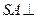 平面ACD.以A为坐标原点,AC、AD、SA分别为
平面ACD.以A为坐标原点,AC、AD、SA分别为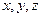 轴建立空间直角坐标系,则易得……………2分
轴建立空间直角坐标系,则易得……………2分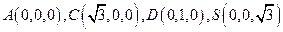 ,
,
(Ⅰ)由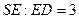 有
有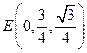 ,……………4分
,……………4分
易得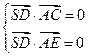 ,从而
,从而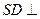 平面ACE.……………………7分
平面ACE.……………………7分
(Ⅱ)由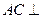 平面
平面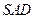 ,二面角
,二面角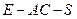 的平面角
的平面角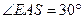 .
.
又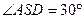 ,则 E为
,则 E为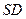 的中点,
的中点,
即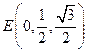 ,………………9分
,………………9分
设平面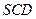 的法向量为
的法向量为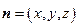
则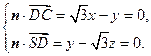 ,令
,令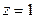 ,得
,得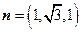 ,…………11分
,…………11分
从而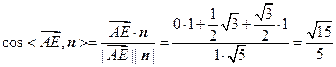 ,…………13分
,…………13分
直线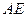 与平面
与平面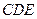 所成角的正弦值大小为
所成角的正弦值大小为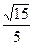 .……………………14分
.……………………14分
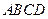 中,由
中,由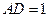 ,
, ,
,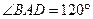 ,
,

易知
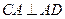 ,…………………2分
,…………………2分又
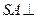 平面
平面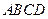 ,所以
,所以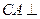 平面
平面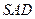 ,
,∴
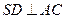 ,
,在直角三角形
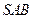 中,易得
中,易得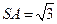 ,
,在直角三角形

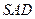 中,
中,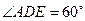 ,
,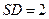 ,
,又
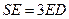 ,∴
,∴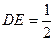 ,
,可得
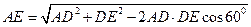
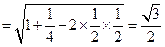 .
.∴
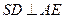 ,
, ……………………6
……………………6 分
分又∵
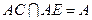 ,∴
,∴
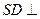 平面
平面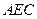 .………7分
.………7分(Ⅱ)由(Ⅰ)可知,
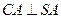 ,
,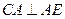 ,
,可知
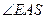 为二面角
为二面角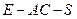 的平面角,
的平面角, 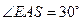 ,此时
,此时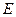 为
为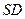 的中点. ……………9分
的中点. ……………9分过
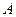 作
作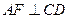
 ,连结
,连结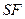 ,则平面
,则平面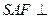 平面
平面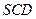 ,
,作

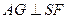 ,则
,则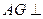 平面
平面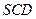 ,连结
,连结
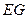 ,
,可得
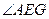 为直线
为直线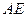 与平面
与平面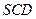 所成的角.
所成的角.因为
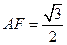 ,
,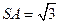 ,
,所以
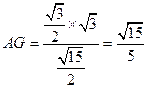 .……
.…… ………12分
………12分在
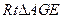 中,
中,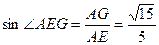
直线
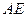 与平面
与平面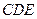 所成角的正弦值大小为
所成角的正弦值大小为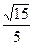 .……………………14分
.……………………14分解法二:依题意易知
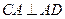 ,
,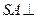 平面ACD.以A为坐标原点,AC、AD、SA分别为
平面ACD.以A为坐标原点,AC、AD、SA分别为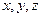 轴建立空间直角坐标系,则易得……………2分
轴建立空间直角坐标系,则易得……………2分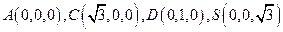 ,
,(Ⅰ)由
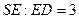 有
有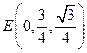 ,……………4分
,……………4分易得
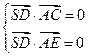 ,从而
,从而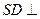 平面ACE.……………………7分
平面ACE.……………………7分(Ⅱ)由
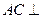 平面
平面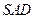 ,二面角
,二面角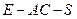 的平面角
的平面角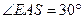 .
.又
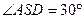 ,则 E为
,则 E为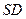 的中点,
的中点, 即
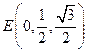 ,………………9分
,………………9分设平面
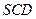 的法向量为
的法向量为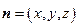
则
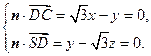 ,令
,令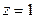 ,得
,得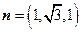 ,…………11分
,…………11分从而
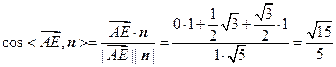 ,…………13分
,…………13分直线
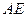 与平面
与平面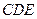 所成角的正弦值大小为
所成角的正弦值大小为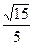 .……………………14分
.……………………14分略

练习册系列答案
相关题目
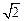 .
.
 ,
,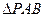 ≌
≌ ,在它的俯视图
,在它的俯视图 中,
中, ,
, ,
, .
. 是直角三角形;⑵求四棱锥
是直角三角形;⑵求四棱锥 的体积.
的体积.
 的直观图与三视图如图所示
的直观图与三视图如图所示 积;
积;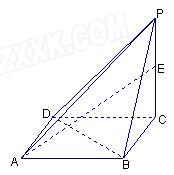

 中,
中, ,
, ,且
,且 (I)设
(I)设 为线段
为线段 的中点,试在线段
的中点,试在线段 上求一点
上求一点 ,使得
,使得 ;
; 的平面角的余弦值.
的平面角的余弦值.
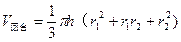 )
)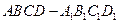 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,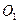 是
是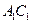 和
和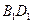 的交点。
的交点。
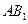 与底面
与底面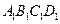 所成的角的大小为
所成的角的大小为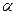 ,二面角
,二面角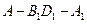 的大小为
的大小为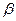 。
。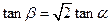 ;
;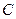 到平面
到平面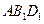 的距离为
的距离为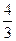 ,求正四棱柱
,求正四棱柱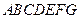 为多面体,平面
为多面体,平面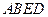 与平面
与平面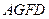 垂直,点
垂直,点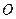 在线段
在线段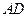 上,
上,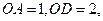
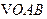 ,△
,△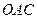 ,△
,△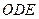 ,△
,△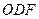 都是正三角形。
都是正三角形。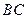 ∥
∥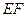 ;
;