题目内容
(本小题满分14分)
如图,四面体ABCD中,O,E分别为BD,BC的中点,CA=CB=CD=BD=2,AB=AD=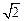 .
.
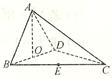
(1)求证:AO⊥平面BCD;
(2)求点E到平面ACD的距离.
如图,四面体ABCD中,O,E分别为BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
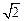 .
.
(1)求证:AO⊥平面BCD;
(2)求点E到平面ACD的距离.
解析:(1)连结OC.因为BO=DO,AB=AD,所以AO⊥BD.因为BO=DO,CB=CD,所以CO⊥BD.
在△AOC中,由已知可得AO=1,CO= .而AC=2,所以
.而AC=2,所以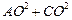 =
=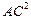 ,所以∠AOC=
,所以∠AOC=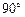 ,即AO⊥OC.因为BD
,即AO⊥OC.因为BD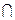 OC=O,所以AO⊥平面BCD.
OC=O,所以AO⊥平面BCD.
(2)设点E到平面ACD的距离为h.因为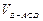 =
=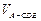 ,所以
,所以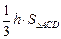 =
=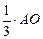
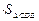 .
.
在△ACD中,CA=CD=2,AD=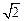 ,所以
,所以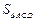 =
=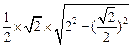 =
=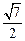 .
.
而AO=1,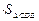 =
=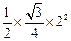 =
=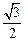 ,所以h=
,所以h=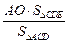 =
=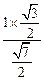 =
=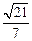 .
.
所以点E到平面ACD的距离为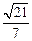 .
.
在△AOC中,由已知可得AO=1,CO=
 .而AC=2,所以
.而AC=2,所以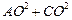 =
=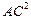 ,所以∠AOC=
,所以∠AOC=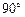 ,即AO⊥OC.因为BD
,即AO⊥OC.因为BD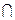 OC=O,所以AO⊥平面BCD.
OC=O,所以AO⊥平面BCD.(2)设点E到平面ACD的距离为h.因为
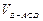 =
=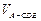 ,所以
,所以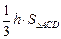 =
=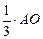
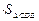 .
.在△ACD中,CA=CD=2,AD=
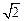 ,所以
,所以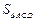 =
=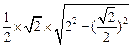 =
=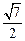 .
.而AO=1,
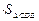 =
=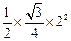 =
=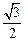 ,所以h=
,所以h=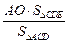 =
=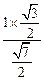 =
=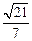 .
.所以点E到平面ACD的距离为
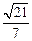 .
.略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
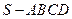 中,底面
中,底面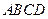 为平行四边形,
为平行四边形,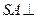 平面
平面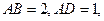
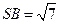
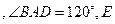 在棱
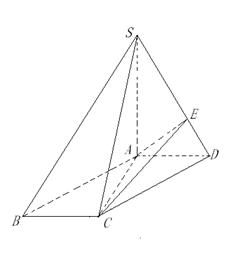
在棱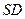 上
上 .
.
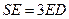 时,求证
时,求证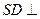 平面
平面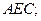
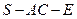 的大小为
的大小为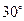 时,求直线
时,求直线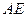 与平面
与平面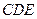 所成角的正弦值.
所成角的正弦值.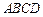 是圆柱
是圆柱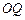 的轴截面,点
的轴截面,点 在圆柱
在圆柱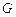 是
是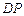 的中点,圆柱
的中点,圆柱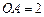 ,侧面积为
,侧面积为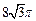 ,
,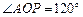 .
.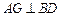 ;
;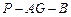 的平面角的余弦值.
的平面角的余弦值.
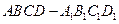 为正
为正 方体,一只青蛙开始在顶点A处,它每次可随意
方体,一只青蛙开始在顶点A处,它每次可随意 跳到相邻三顶点之一,若在五次内跳到
跳到相邻三顶点之一,若在五次内跳到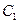 点,则停止跳动;若5次内不能跳到
点,则停止跳动;若5次内不能跳到 次也停止跳动,求:
次也停止跳动,求: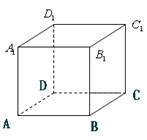
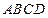 为直角梯形,
为直角梯形,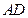 //
//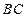 ,
,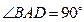 ,
, 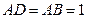 ,
, 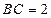 ,
, 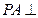 平面
平面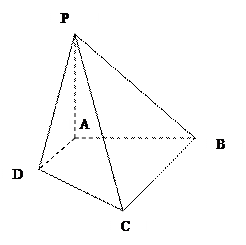
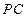 与
与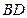 所成的角为
所成的角为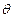 ,且
,且 ,求
,求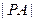 ;
;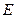 为
为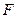 ,使
,使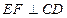 ?
?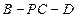 的大小.
的大小.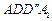 和
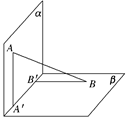
和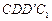 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使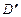 与
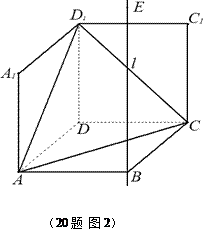
与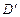 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设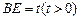 (图2)。
(图2)。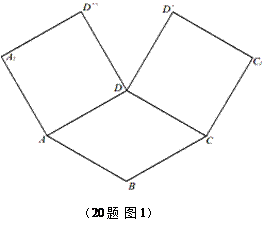
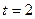 时,求
时,求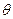 的余弦值;
的余弦值;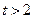 时在线段
时在线段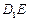 上是否存在点
上是否存在点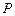 ,使平面
,使平面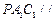 平面
平面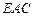 ,若存在,求出
,若存在,求出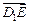 所成的比
所成的比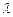 ;若不存在,请说明理由。
;若不存在,请说明理由。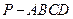 中,底面ABCD是矩形,PA=AD=4,AB=2,PB=
中,底面ABCD是矩形,PA=AD=4,AB=2,PB=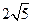 ,PD=
,PD=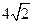 。E是PD的中点。
。E是PD的中点。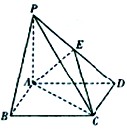
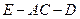 的平面角的大小的余弦值;
的平面角的大小的余弦值;  ,
,