题目内容
【题目】已知函数 ![]() . (Ⅰ)求该函数的周期和最大值;
. (Ⅰ)求该函数的周期和最大值;
(Ⅱ)该函数的图象经过怎样的平移和伸缩变换可以得到y=sinx(x∈R)的图象.
【答案】解:(Ⅰ) ![]() 所以,函数的周期
所以,函数的周期 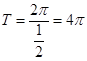 ,函数的最大值为ymax=2..
,函数的最大值为ymax=2..
(Ⅱ)该函数的图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再把所得图象上所有点向右平移
倍(纵坐标不变),再把所得图象上所有点向右平移 ![]() 个单位,可以得到y=sinx(x∈R)的图象.
个单位,可以得到y=sinx(x∈R)的图象.
或将该函数的图象上所有的点向右平移 ![]() 个单位,再把所得图象上所有点的横坐标缩短到原来的
个单位,再把所得图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),可以得到y=sinx(x∈R)的图象
倍(纵坐标不变),可以得到y=sinx(x∈R)的图象
【解析】(Ⅰ)利用两角和的正弦函数化简表达式,然后求解求该函数的周期和最大值;(Ⅱ)利用三角函数的图形的变换原则,推出结果即可.
【考点精析】本题主要考查了五点法作函数y=Asin(ωx+φ)的图象的相关知识点,需要掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)才能正确解答此题.

练习册系列答案
相关题目
