题目内容
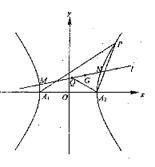
已知中心在原点，左、右顶点A1、A2在x轴上，离心率为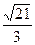
的双曲线C经过点P（6,6），动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N，Q为线段MN的中点。
（1）求双曲线C的标准方程
（2）当直线l的斜率为何值时，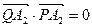
。
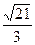的双曲线C经过点P（6,6），动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N，Q为线段MN的中点。（1）求双曲线C的标准方程
（2）当直线l的斜率为何值时，
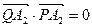。（1）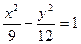
（2）
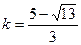
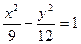
（2）
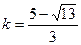
本小题考查双曲线标准议程中各量之间关系，以及直线与双曲线的位置关系。
（1）设双曲线C的方程为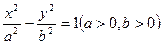
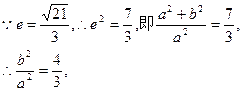
又P（6,6）在双曲线C上，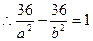
由①、②解得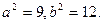
所以双曲线C的方程为。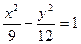
（2）由双曲线C的方程可得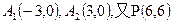
所以△A1PA2的重点G（2,2）
设直线l的方程为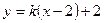
代入C的方程，整理得
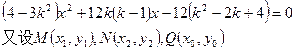
整理得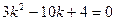
解得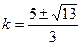
由③，可得
解得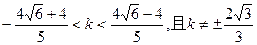
由④、⑤，得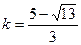
（1）设双曲线C的方程为
|
|
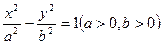
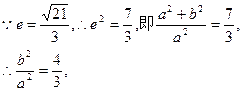
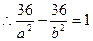由①、②解得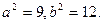所以双曲线C的方程为
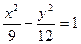。（2）由双曲线C的方程可得
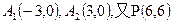
所以△A1PA2的重点G（2,2）
设直线l的方程为
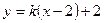代入C的方程，整理得
|
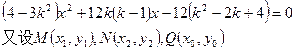
整理得
|
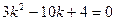
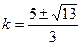由③，可得
|
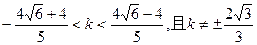由④、⑤，得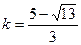
练习册系列答案
阅读快车系列答案
相关题目
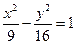的右顶点为A，右焦点为F，过点F平行双曲线的一条渐近线的直线与双曲线交于点B，则△AFB的面积为 。
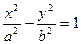(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(－1,0)到直线l的距离之和s≥
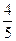c.求双曲线的离心率e的取值范围．
：
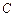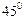后，求得到的曲线
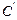的方程；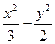
=1截得的弦长为4,求直线l的方程.
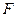为双曲线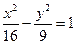
的左焦点，在
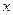轴上
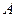，以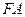
为直径的圆与双曲线左、右两支在
、
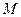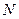，则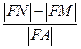
的值为（ ）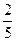
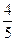
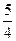
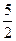
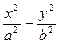=1的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，若△ABF2为锐角
三角形，则该双曲线的离心率e的取值范围是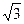 
) C .(
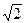－1,1+