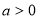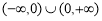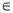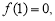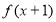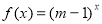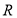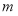题目内容
设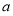 是实数,
是实数,
(1)试确定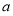 的值,使
的值,使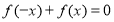 成立;
成立;
(2)求证:不论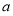 为何实数,
为何实数, 均为增函数
均为增函数
(1)1;(2)证明见试题解析
【解析】
试题分析:(1) 成立,可以直接代入
成立,可以直接代入 的表达式,解出
的表达式,解出 ,即可,也可以由
,即可,也可以由 成立,得
成立,得 为奇函数,从而
为奇函数,从而 ,由此也可很快求出
,由此也可很快求出 (2)要根据增函数的定义证明,设
(2)要根据增函数的定义证明,设 ,由此证明出
,由此证明出 ,为了此目的,作差
,为了此目的,作差 ,证明
,证明
试题解析:(1)由题知 ,则有
,则有
 ,故
,故 的值为1 8分
的值为1 8分
另【解析】
由 成立,得
成立,得 为奇函数,从而
为奇函数,从而 ,即
,即
(2)证明:由题意知 ,在
,在 上任取两个值
上任取两个值 且
且 ,则
,则
 ,
,
由 ,且
,且 为R上的增函数得
为R上的增函数得 ,
, ,
,
则 ,即
,即 ,故不论
,故不论 为何实数,
为何实数, 均为增函数 16分
均为增函数 16分
考点:(1)函数的解析式或奇函数的定义;(2)增函数

练习册系列答案
相关题目