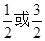题目内容
若P是双曲线 :
: 和圆
和圆 :
: 的一个交点且
的一个交点且
 ,其中
,其中 是双曲线
是双曲线 的两个焦点,则双曲线
的两个焦点,则双曲线 的离心率为
的离心率为
A. | B. | C.2 | D.3 |
B
解析试题分析:由题意, ,且
,且
 ,所以
,所以 ,
, ,
,
设 ,
, .选B.
.选B.
考点:双曲线的应用
点评:本题考查双曲线的离心率的求法,解题时要认真审题,灵活运用双曲线的性质,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个顶点的坐标 ,焦距的一半为3的椭圆的标准方程是( )
,焦距的一半为3的椭圆的标准方程是( )
A. | B. | C. | D. |
椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点 、
、 是它的焦点,长轴长为
是它的焦点,长轴长为 ,焦距为
,焦距为 ,静放在点
,静放在点 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点 时,小球经过的路程是( )
时,小球经过的路程是( )
A. | B. | C. | D.以上答案均有可能 |
若抛物线 的离心率
的离心率 ,则该抛物线准线方程是 ( )
,则该抛物线准线方程是 ( )
A. | B. | C. | D. |
等轴双曲线 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 与抛物线
与抛物线 的准线交于
的准线交于 两点,
两点,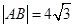 ;则
;则 的实轴长为( )
的实轴长为( )
A. | B. | C. | D. |
抛物线 的准线方程是( )
的准线方程是( )
A. | B. | C. | D. |
 和
和 轴正方向交点为A,和
轴正方向交点为A,和 轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )
轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )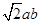



 的两个焦点分别为
的两个焦点分别为 、
、 ,若曲线
,若曲线 满足
满足 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线