题目内容
设椭圆 和
和 轴正方向交点为A,和
轴正方向交点为A,和 轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )
轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )
A.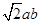 | B. | C. | D. |
D
解析试题分析:由于点P是椭圆 和上的在第一象限内的点,
和上的在第一象限内的点,
设P为(acosa,bsina)即x="acosa" y="bsina" (0<a<π),
这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和,
对于三角形OAP有面积S1= absinα,对于三角形OBP有面积S2=
absinα,对于三角形OBP有面积S2= abcosα,∴四边形的面积S=S1+S2=
abcosα,∴四边形的面积S=S1+S2= ab(sinα+cosα)=
ab(sinα+cosα)= absin(a+
absin(a+ ),
),
其最大值就应该为 ab,并且当且仅当a=
ab,并且当且仅当a= 时成立.所以,面积最大值
时成立.所以,面积最大值 .故选D.
.故选D.
考点:椭圆的标准性质
点评:本题主要考查了椭圆的简单性质,解答的关键在于利用椭圆的参数方程设出椭圆上一点的坐标,利用三角函数的有界性求最值.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
已知直线 ,
, ,过
,过 的直线
的直线 与
与 分别交于
分别交于 ,若
,若 是线段
是线段 的中点,则
的中点,则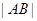 等于( )
等于( )
| A.12 | B. | C. | D. |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率为
的焦点重合,且双曲线的离心率为 ,则此双曲线的方程为
,则此双曲线的方程为
A. | B. | C.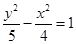 | D. |
双曲线 的渐近线方程是( )
的渐近线方程是( )
A. | B. | C. | D. |
若P是双曲线 :
: 和圆
和圆 :
: 的一个交点且
的一个交点且
 ,其中
,其中 是双曲线
是双曲线 的两个焦点,则双曲线
的两个焦点,则双曲线 的离心率为
的离心率为
A. | B. | C.2 | D.3 |
 ,
, 分别是双曲线
分别是双曲线 :
:
 的两个焦点,双曲线
的两个焦点,双曲线 :
: 的一个交点为
的一个交点为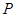 ,且
,且 ,那么双曲线
,那么双曲线


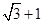
 的离心率为
的离心率为
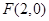 是右焦点.若
是右焦点.若 为双曲线上关于原点对称的两点,且
为双曲线上关于原点对称的两点,且 ,则直线
,则直线 的斜率是( )
的斜率是( )



 围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则
围成的区域(含边界)为Ωn(n=1,2,…),当点(x,y)分别在Ω1,Ω2,…上时,x+y的最大值分别是M1,M2,…,则 Mn=( )
Mn=( )

 与点
与点 ,过C的焦点且切率为k的直线与C交于A、B两点,若
,过C的焦点且切率为k的直线与C交于A、B两点,若 ,则
,则 ( )
( )
 (B)
(B) (C)
(C) (D)
(D)