题目内容
20.已知函数$f(x)=\frac{x+2a-1}{{{x^2}+1}}$为奇函数,及lg2=0.3010,lg2.015=0.3043.(1)求实数a的值;
(2)证明函数f(x)在区间[1,+∞)上是减函数;
(3)求最小的正整数n,使得f(1+0.01×2n)+f(-2016)<f(0).
分析 (1)根据函数奇偶性的性质,利用f(0)=0,即可求实数a的值;
(2)利用函数单调性的定义即可证明函数f(x)在区间[1,+∞)上是减函数;
(3)根据函数奇偶性和单调性的关系,将不等式进行转化求解即可.
解答 解:(1)由f(0)=0,求得$a=\frac{1}{2}$…(3分)
(2)由(1)可知$f(x)=\frac{x}{{{x^2}+1}}$,设x1,x2∈[1,+∞),设x1<x2,则…(4分)$f({x_1})-f({x_2})=\frac{x_1}{x_1^2+1}-\frac{x_2}{x_2^2+1}=\frac{{{x_1}(x_2^2+1)-{x_2}(x_1^2+1)}}{(x_1^2+1)(x_2^2+1)}=\frac{{({x_2}-{x_1})({x_1}{x_2}-1)}}{(x_1^2+1)(x_2^2+1)}$,
∵1≤x1<x2,∴f(x1)>f(x2),
∴f(x)在区间[1,+∞)上是减函数; …(7分)
(3)∵f(x)为奇函数,∴f(0)=0,f(-2016)=-f(2016),…(8分)
所以原式可化为f(1+0.01×2n)<f(2016),
由(2)可知函数f(x)在[1,+∞)上单调递减,且1+0.01×2n>1,
∴1+0.01×2n>2016,即2n>201500,…(10分)
两边取对数,得nlg2>lg2.015+5,即0.3010n>5.3043,
解得n>17.62,故最小的正整数n的值为18.…(12分)
点评 本题主要考查函数奇偶性的应用以及函数单调性的证明,利用定义法是解决本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
15.在△ABC中,a=9,b=3$\sqrt{3}$; A=120°,则sin(π-B)等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
5.下列函数中,值域为(0,+∞)的是( )
| A. | y=$\sqrt{x}$ | B. | y=$\frac{1}{\sqrt{x}}$ | C. | y=$\frac{1}{x}$ | D. | y=x2+1 |
12.已知集合A={x|-1≤x≤1},B={x|x>0},则A∩(∁RB)=( )
| A. | {x|-1≤x≤0} | B. | {x|-1≤x<0} | C. | {x|-1≤x≤1} | D. | {x|x≤1} |
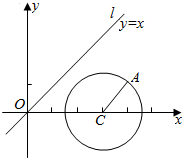 已知圆C的圆心为(3,0),且经过点A(4,1),直线l:y=x.
已知圆C的圆心为(3,0),且经过点A(4,1),直线l:y=x. 已知菱形ABCD中,∠DAB=60°,点G是正△PAD的边AD的中
已知菱形ABCD中,∠DAB=60°,点G是正△PAD的边AD的中