在△ABC中.a=9.b=3$\sqrt{3}$, A=120°.则sinA．$\frac{1}{2}$B．-$\frac{1}{2}$C．$\frac{{\sqrt{3}}}{2}$D．-$\frac{{\sqrt{3}}}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

15．在△ABC中，a=9，b=3$\sqrt{3}$； A=120°，则sin（π-B）等于（　　）

A．

$\frac{1}{2}$

B．

-$\frac{1}{2}$

C．

$\frac{{\sqrt{3}}}{2}$

D．

-$\frac{{\sqrt{3}}}{2}$

分析利用已知及正弦定理即可求得sinB，结合诱导公式即可得解．

解答解：由正弦定理：$\frac{a}{sinA}=\frac{b}{sinB}$，可得sinB=$\frac{bsinA}{a}$=$\frac{3\sqrt{3}×\frac{\sqrt{3}}{2}}{9}$=$\frac{1}{2}$，
解得：sin（π-B）=sinB=$\frac{1}{2}$．
故选：A．

点评本题主要考查了正弦定理，诱导公式的综合应用，属于基础题．

练习册系列答案

	A．	V₁+V₂=V₃		B．	$\frac{1}{V_1}+\frac{1}{V_2}=\frac{1}{V_3}$
	C．	$V_1^2+V_2^2=V_3^2$		D．	$\frac{1}{V_1^2}+\frac{1}{V_2^2}=\frac{1}{V_3^2}$

6．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左、右焦点分别为F₁，F₂，过F₂的直线与双曲线C的右支相交于P，Q两点，若PQ⊥PF₁，且|PF₁|=|PQ|，则双曲线的离心率e=（　　）

3．用区间表示下列集合：
（1）$\{x\left|{-\frac{1}{2}≤x＜5\}}\right.$=[-$\frac{1}{2}$，5）．
（2）{x|x＜1或2＜x≤3}=（-∞，1）∪（2，3]．

10．给定下列命题：
①“若k＞0，则方程x²+2x-k=0有实数根”的逆否命题；
②“若A=B，则sinA=sinB”的逆命题；
③“若$\frac{1}{a}＜\frac{1}{b}＜0，则\;ab＜b$²”的逆否命题；
④“若xy=0，则x，y中至少有一个为零”的否命题．
⑤“若$\frac{b}{a}＞\frac{a}{b}，则\;a＜b＜0$”的逆命题．
其中真命题的序号是①③④．

20．已知函数$f（x）=\frac{x+2a-1}{{{x^2}+1}}$为奇函数，及lg2=0.3010，lg2.015=0.3043．
（1）求实数a的值；
（2）证明函数f（x）在区间[1，+∞）上是减函数；
（3）求最小的正整数n，使得f（1+0.01×2ⁿ）+f（-2016）＜f（0）．

7．已知A，B，C，D是球面上的四个点，其中A，B，C在同一圆周上，若D不在A，B，C所在的圆周上，则从这四点中的任意两点的连线中取2条，这两条直线是异面直线的概率等于（　　）

4．设等比数列{a_n}的前n项和S_n，已知${a_3}=\frac{1}{8}$，且${S_2}+\frac{1}{16}，{S_3}，{S_4}$成等差数列．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设${b_n}={a_n}{log_{\frac{1}{2}}}{a_n}$，求数列{b_n}的前n项和T_n．

5．

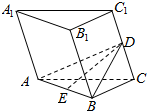在正三棱柱ABC-A₁B₁C₁中，E是AB的中点，D是CC₁上一点．
（I）求证：A₁B₁∥平面DAB；
（Ⅱ）求证：A₁B₁⊥DE．

试题分类