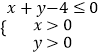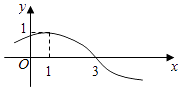��Ŀ����
����Ŀ��Ϊ�о���Ůͬѧ�ռ����������IJ��죬����ʦ�Ӹ�һ�꼶���ѡȡ��20��������20��Ů�������пռ�ͼ��ʶ����ԣ��õ��ɼ���Ҷͼ���£��ٶ��ɼ����ڵ���80�ֵ�ͬѧΪ���ռ���������ͻ����������80�ֵ�ͬѧΪ���ռ����������������� 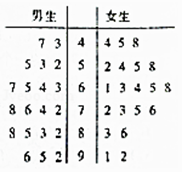
��1���������2��2��������
�ռ���������ͻ�� | �ռ������������� | �ϼ� | |
���� |
|
|
|
�� |
|
|
|
�ϼ� |
|
|
|
��2���ж��Ƿ���90%�İ�����Ϊ���ռ���������ͻ�������Ա��йأ�
��3���ӡ��ռ���������ͻ������ͬѧ�����ѡȡ����2����Ů��2���������гɼ�����90�ֵ�����Ϊ�Σ�����������εķֲ��к���ѧ������ ���湫ʽ���ٽ�ֵ�������ο��� ![]()
P��X2��k�� | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
���𰸡�
��1��
�ռ���������ͻ�� | �ռ������������� | �ϼ� | |
���� | 7 | 13 | 20 |
�� | 4 | 16 | 20 |
�ϼ� | 11 | 29 | 40 |
��2���ɹ�ʽ 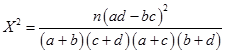 �������X2��1.129��
�������X2��1.129��
��ΪX2��2.706������û��90%�İ�����Ϊ���ռ���������ͻ�������Ա��й�
��3���⣺ ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
���Ԧεķֲ����ǣ�
�� | 0 | 1 | 2 | 3 | 4 |
P | | | | | |
��ѧ�����ǣ� ![]()
����������1��2��2���������£�������X2���㹫ʽ�ɵý��ۣ���3�����û����¼��������¼��ĸ��ʼ��㹫ʽ�ɵæεķֲ��м�����ѧ�������㹫ʽ��
�����㾫����������Ҫ��������ɢ�������������ֲ��е����֪ʶ�㣬��Ҫ�������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в�����ȷ�����⣮

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�