题目内容
【题目】已知| 
|=4，| 
|=3，（2 ﹣3 ）（2 + ）=61．
（1）求 与 的夹角θ；
（2）求| + |和| ﹣ |．
【答案】
（1）解：由（2 
﹣3 
）（2 + ）=61，
得4| |2﹣4 ﹣3| |2=61；
又| |=4，| |=3，代入上式求得 =﹣6，
∴cosθ=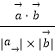 
= 
=﹣ 
，
又θ∈[0°，180°]，
∴θ=120°
（2）解：| + |2=（ + ）2=| |2+2 +| |2=42+2×（﹣6）+32=13，
∴| + |= 
；
同理，| ﹣ |= 
= 
【解析】（1）由向量的线性运算可计算出向量a和向量b的数量积的值为-6，再根据向量的数量积运算公式推导出cosθ的值，进而得到θ。（2）由向量的线性运算整理可得出结果。
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】为研究男女同学空间想象能力的差异，孙老师从高一年级随机选取了20名男生、20名女生，进行空间图形识别测试，得到成绩茎叶图如下，假定成绩大于等于80分的同学为“空间想象能力突出”，低于80分的同学为“空间想象能力正常”．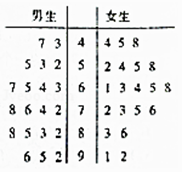 
（1）完成下面2×2列联表，
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
（2）判断是否有90%的把握认为“空间想象能力突出”与性别有关；
（3）从“空间想象能力突出”的同学中随机选取男生2名、女生2名，记其中成绩超过90分的人数为ξ，求随机变量ξ的分布列和数学期望． 下面公式及临界值表仅供参考： 
P（X2≥k） | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
