题目内容
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a>0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数),若直线l与圆C恒有公共点,求实数a的取值范围.
(t为参数),若直线l与圆C恒有公共点,求实数a的取值范围.
【答案】解:由ρ=2acosθ得ρ2=2aρcosθ,
∴圆C的标准方程为x2+y2=2ax,
把 ![]() (t为参数)代入圆的方程可得169t2﹣(14+10a)t+2﹣2a=0,
(t为参数)代入圆的方程可得169t2﹣(14+10a)t+2﹣2a=0,
∴△=(14+10a)2﹣4×169×(2﹣2a)≥0,
解得:﹣17≤a≤ ![]() ,
,
又a>0,
∴0<a≤ ![]() .
.
∴实数a的取值范围为(0, ![]() ]
]
【解析】利用圆的极坐标方程和标准方程的转化整理的到圆的标准方程,再把直线的参数方程代入圆的方程,整理可得169t2﹣(14+10a)t+2﹣2a=0,令△≥0解出a的取值范围。
【考点精析】认真审题,首先需要了解直线与圆的三种位置关系(直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点).

【题目】为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”. 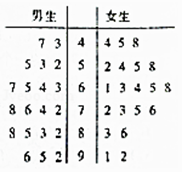
(1)完成下面2×2列联表,
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(2)判断是否有90%的把握认为“空间想象能力突出”与性别有关;
(3)从“空间想象能力突出”的同学中随机选取男生2名、女生2名,记其中成绩超过90分的人数为ξ,求随机变量ξ的分布列和数学期望. 下面公式及临界值表仅供参考: ![]()
P(X2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |