Question

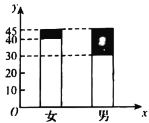
【题目】某校在高一部分学生中调查男女同学对某项体育运动的喜好情况，其二维条形图如图（黑色代表喜好，白色代表不喜好）.

（1）写出列联表；

（2）能否有99%的把握认为喜好这项体育运动与性别有关；

（3）在这次调查中从喜好这项体育活动的一名男生和两名女生中任选两人进行专业培训，求恰是一男一女的概率.

附：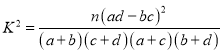

	0.25	0.010	0.005	0.001
	5.024	6.635	7.879	10.83

Answer 1

【答案】（1）见解析（2）没有99%把握认为喜好这项体育运动与性别有关（3）

【解析】

（1）观察二维条形图得到所需数据，由此写出列联表即可；

（2）根据列联表中的数据计算，对照数表即可得出结论；

（3）通过列举法分别写出任选两人的情况和选一名男生和一名女生的情况，再由古典概型的概率公式计算即可.

（1）观察二维条形图可得，

男生总共45人，其中喜好这项运动的有15人，不喜好的有30人；

女生总共45人，其中喜好这项运动的有5人，不喜好的有40人.

由此写出列联表如下：

列联表：单位；人

	喜欢	不喜欢	总计
男	15	30	45
女	5	40	45
总计	20	70	90

（2）.

所以没有99%把握认为喜好这项体育运动与性别有关.

（3）设喜好这项体育活动的一名男生和两名女生记为，，.

任选两人的情况为：，，，

选一名男生和一名女生的情况为：，，

所以，

即恰是一男一女的概率为.