题目内容
8.已知函数f(x)=x4+(2-λ)x2+2-λ,问是否存在λ,使函数f(x)在(-∞,-1)上是减函数,在(-1,0)上是增函数.分析 求f′(x)=x(4x2+4-2λ),所以根据函数f(x)的单调性即可得到:x∈(-∞,-1)时,4x2+4-λ2≥0;x∈(-1,0)时,4x2+4-2λ≤0,这样即可得出x=-1时4x2+4-2λ=0,代入x=-1,求出λ即可.
解答 解:f′(x)=x(4x2+4-2λ);
要使f(x)在(-∞,-1)是减函数,在(-1,0)是增函数,则:
x∈(-∞,-1)时f′(x)≤0,x∈(-1,0)时f′(x)≥0;
∴x∈(-∞,-1)时,4x2+4-2λ≥0;x∈(-1,0)时,4x2+4-2λ≤0;
∴x=-1时,4+4-2λ=0,λ=4;
即存在λ=4,使函数f(x)在(-∞,-1)上是减函数,在(-1,0)上是增函数.
点评 考查函数单调性和函数导数符号的关系,以及要熟悉二次函数的图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知实数x∈{1,2,3,4,5,6,7,8},执行如图所示的程序框图,则输出的x不小于121的概率为( )
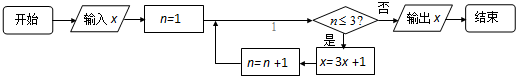
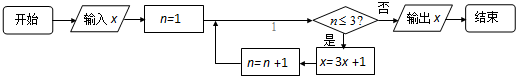
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
8.若方程(x-1)4+mx-m-2=0各个实根x1,x2,…,xk(k≤4,k∈N*)所对应的点$({x_i},\frac{2}{{{x_i}-1}})$,(i=1,2,…,k)均在直线y=x的同侧,则实数m的取值范围是( )
| A. | (-1,7) | B. | (-∞,-7)∪(-1,+∞) | C. | (-7,1) | D. | (-∞,1)∪(7,+∞) |