题目内容
3.已知公差不为0的等差数列{an}中,a1,a2,a5依次成等比数列,则$\frac{a_5}{a_1}$=9.分析 先利用等差数列的通项公式,用a1和d分别表示出等差数列的a1,a2,a5,进而利用等比数列的性质建立等式,求得a1和d的关系,进而再利用等差数列的通项公式化简$\frac{{a}_{5}}{{a}_{1}}$,将求出的a1和d的关系代入,合并约分后即可求出所求式子的值.
解答 解:∵a1,a2,a5成等比数列,
∴a22=a1•a5,即(a1+d)2=a1(a1+4d),
由d≠0,
解得:2a1=d,
∴$\frac{{a}_{5}}{{a}_{1}}$=$\frac{\frac{1}{2}d+4d}{\frac{1}{2}d}$=9.
故答案为:9.
点评 此题考查了等比数列的性质,以及等比数列的通项公式,熟练掌握性质及通项公式是解本题的关键.

练习册系列答案
相关题目
13.已知F为抛物线C:y2=4x的焦点,点E在点C的准线上,且在x轴上方,线段EF的垂直平分线于C的准线交于点Q(-1,$\frac{3}{2}$),与C交于点P,则△PEF的面积为( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
11.i是虚数单位,复数$\frac{5-2i}{2+5i}$=( )
| A. | -i | B. | i | C. | -$\frac{21}{29}$-$\frac{20}{29}$i | D. | -$\frac{4}{21}$+$\frac{10}{21}$i |
2.定义A*B,B*C,C*D,D*A的运算分别对应图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是( )


| A. | B*D A*D | B. | B*D A*C | C. | B*C A*D | D. | C*D A*D |
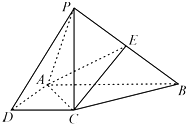 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,