Question

【题目】在平面直角坐标系xoy中，已知圆C1：（x+3）2+（y﹣1）2=4和圆C2：（x﹣4）2+（y﹣5）2=4
（1）若直线l过点A（4，0），且被圆C1截得的弦长为2 ，求直线l的方程
（2）设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2 ， 它们分别与圆C1和C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，求所有满足条件的点P的坐标．

Answer 1

【答案】
（1）解：由于直线x=4与圆C1不相交；

∴直线l的斜率存在，设l方程为：y=k（x﹣4）

圆C1的圆心到直线l的距离为d，∵l被⊙C1截得的弦长为2

∴d= =1

d= 从而k（24k+7）=0即k=0或k=﹣

∴直线l的方程为：y=0或7x+24y﹣28=0

（2）解：设点P（a，b）满足条件，

由题意分析可得直线l1、l2的斜率均存在且不为0，

不妨设直线l1的方程为y﹣b=k（x﹣a），k≠0

则直线l2方程为：y﹣b=﹣ （x﹣a）

∵⊙C1和⊙C2的半径相等，及直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，

∴⊙C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等

即 =

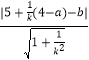
整理得|1+3k+ak﹣b|=|5k+4﹣a﹣bk|

∴1+3k+ak﹣b=±（5k+4﹣a﹣bk）即（a+b﹣2）k=b﹣a+3或（a﹣b+8）k=a+b﹣5

因k的取值有无穷多个，所以 或

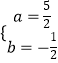解得 或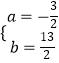

这样的点只可能是点P1（ ，﹣ ）或点P2（﹣ ， ）

【解析】（1）因为直线l过点A（4，0），故可以设出直线l的点斜式方程，又由直线被圆C1截得的弦长为2 ，根据半弦长、半径、弦心距满足勾股定理，我们可以求出弦心距，即圆心到直线的距离，得到一个关于直线斜率k的方程，解方程求出k值，代入即得直线l的方程．（2）与（1）相同，我们可以设出过P点的直线l1与l2的点斜式方程，由于两直线斜率为1，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，故我们可以得到一个关于直线斜率k的方程，解方程求出k值，代入即得直线l1与l2的方程．