题目内容
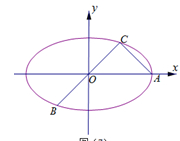
如图,在平面直角坐标系 中,已知
中,已知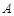 ,
, ,
, 是椭圆
是椭圆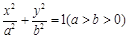 上不同的三点,
上不同的三点,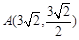 ,
,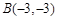 ,
, 在第三象限,线段
在第三象限,线段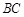 的中点在直线
的中点在直线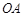 上.
上.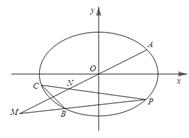
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点 在椭圆上(异于点
在椭圆上(异于点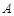 ,
, ,
, )且直线PB,PC分别交直线OA于
)且直线PB,PC分别交直线OA于 ,
,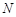 两点,证明
两点,证明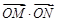 为定值并求出该定值.
为定值并求出该定值.
(1)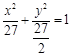 ;(2)
;(2)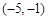 ;(3)
;(3)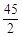 .
.
解析试题分析:(1)已知椭圆过两点,可把两点坐标代入方程列出关于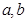 的方程组,然后把
的方程组,然后把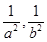 分别作为整体,方程组就变为二元一次方程组,从而可很快解得
分别作为整体,方程组就变为二元一次方程组,从而可很快解得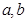 ;(2)关键是线段
;(2)关键是线段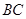 的中点在直线
的中点在直线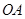 上,可设
上,可设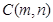 ,由线段
,由线段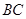 中点为
中点为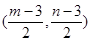 ,而直线
,而直线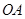 的方程可求得
的方程可求得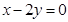 ,代入可得
,代入可得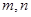 的一个方程,点
的一个方程,点 坐标代入椭圆方程又得另一方程,联立可解得
坐标代入椭圆方程又得另一方程,联立可解得 点坐标
点坐标 ;(3)这类问题我们采取设而不求的方法,设
;(3)这类问题我们采取设而不求的方法,设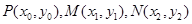 ,
,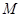 在直线
在直线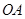 上,则
上,则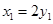 ,同理
,同理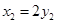 ,
,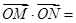
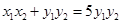 ,下面我们想办法把
,下面我们想办法把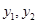 用
用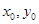 表示出来,这可由
表示出来,这可由 共线,
共线,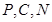 共线得到,这里要考查同学计算能力,只要计算正确,就能得出正确结论.
共线得到,这里要考查同学计算能力,只要计算正确,就能得出正确结论.
试题解析:(1)由已知,得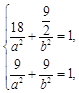 解得
解得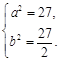 2分
2分
所以椭圆的标准方程为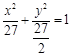 . 3分
. 3分
(2)设点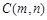
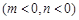 ,则
,则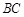 中点为
中点为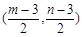 .
.
由已知,求得直线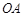 的方程为
的方程为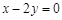 ,从而
,从而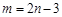 .①
.①
又∵点 在椭圆上,∴
在椭圆上,∴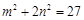 .②
.②
由①②,解得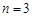 (舍),
(舍),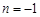 ,从而
,从而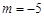 . 5分
. 5分
所以点 的坐标为
的坐标为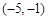 . 6分
. 6分
(3)设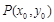 ,
,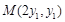 ,
,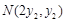 .
.
∵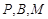 三点共线,∴
三点共线,∴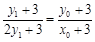 ,整理,得
,整理,得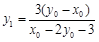 . 8分
. 8分
∵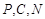 三点共线,∴
三点共线,∴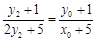 ,整理,得
,整理,得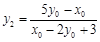 . 10分
. 10分
∵点 在椭圆上,∴
在椭圆上,∴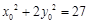 ,
,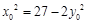 .
.
从而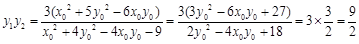 . 14分
. 14分
所以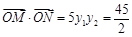 . 15分
. 15分
∴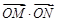 为定值,定值为
为定值,定值为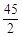 . 16分
. 16分
考点:(1)椭圆的标准方程;(2)中点问题;(3)定值问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
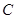 :
: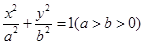 的右焦点为
的右焦点为 ,短轴的一个端点
,短轴的一个端点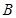 到
到 的距离等于焦距.
的距离等于焦距.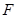 的直线
的直线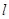 与椭圆
与椭圆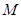 ,
,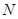 ,是否存在直线
,是否存在直线 与△
与△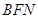 的面积比值为
的面积比值为 ?若存在,求出直线
?若存在,求出直线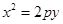
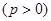 上的点
上的点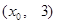 到焦点的距离等于4,直线
到焦点的距离等于4,直线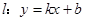 与抛物线相交于不同的两点
与抛物线相交于不同的两点 、
、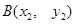 ,且
,且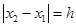 (
(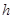 为定值).设线段
为定值).设线段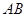 的中点为
的中点为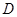 ,与直线
,与直线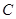 ..
..
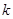 、
、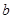 表示出
表示出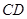 垂直于
垂直于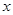 轴;
轴;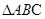 的面积,证明
的面积,证明
 ,求点A的坐标;
,求点A的坐标;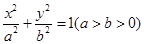 的离心率是
的离心率是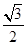 .
.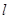 ,使点C(2,0)关于直线
,使点C(2,0)关于直线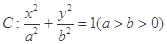 的离心率为
的离心率为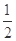 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。 的标准方程;
的标准方程;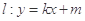 与椭圆
与椭圆 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.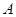 、
、 、
、 是长轴长为
是长轴长为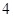 的椭圆
的椭圆 上的三点,点
上的三点,点 过椭圆中心
过椭圆中心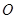 ,且
,且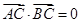 ,
,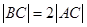 .
.
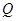 ,使得
,使得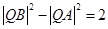 ?若存在,有几个(不必求出
?若存在,有几个(不必求出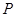 ,作圆
,作圆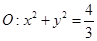 的两条线,切点分别为
的两条线,切点分别为 、
、 ,,若直线
,,若直线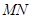 在
在 轴、
轴、 轴上的截距分别为
轴上的截距分别为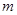 、
、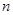 ,证明:
,证明: 为定值.
为定值.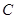 的中心在原点,右焦点为
的中心在原点,右焦点为 ,渐近线方程为
,渐近线方程为 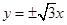 .
.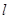 :
: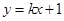 与双曲线
与双曲线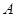 、
、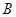 两点,问:当
两点,问:当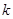 为何值时,以
为何值时,以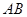 为直径的圆过原点;
为直径的圆过原点;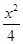 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.