题目内容
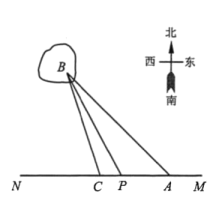
【题目】如图，某沿海地区计划铺设一条电缆联通A，B两地，A地位于东西方向的直线MN上的陆地处，B地位于海上一个灯塔处，在A地用测角器测得
，在A地正西方向4km的点C处，用测角器测得
.拟定铺设方案如下：在岸MN上选一点P，先沿线段AP在地下铺设，再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km，设
，
，铺设电缆的总费用为
万元.
（1）求函数的解析式；
（2）试问点P选在何处时，铺设的总费用最少，并说明理由.
【答案】（1）
，其中
（2）当点P选在距离A地
处时，铺设的总费用最少，详见解析.
【解析】
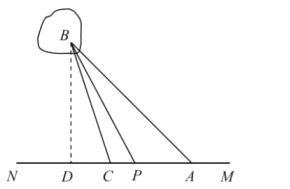
（1）过B作MN的垂线，垂足为D，根据题中条件，得到
，
，由
，得到
，
，
，进而得到
，化简即可得出结果；
（2）根据（1）的结果，先设
，，对
求导，用导数的方法研究其单调性，即可求出最值.
（1）过B作MN的垂线，垂足为D.
在
中，
，则.
在
中，
，
所以.
因为
，所以
，
所以
.
由，则，.
由
，得.
所以，
即，其中.
（2）设，，
则
.
令
，得
，所以
.
列表如下：
|
|
|
|
|
| 0 |
|
h(θ) | ↘ | 极小值 | ↗ |
所以当时，取得最小值
，
所以
取得最小值
，此时
.
答：当点P选在距离A地处时，铺设的总费用最少，且为万元.
练习册系列答案
相关题目
