题目内容
【题目】在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是（写出所有正确结论的编号）.
①矩形；
②不是矩形的平行四边形；
③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；
④每个面都是等边三角形的四面体；
⑤每个面都是直角三角形的四面体.
【答案】①③④⑤
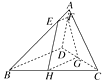
【解析】本题中①③④⑤只要能举一例说明正确即可，如图长方体 
中，四边形 
是矩形，四面体 
有三个面是直角三角形，第四个面 
是等腰三角形，四面体 
每个面都是等腰三角形，四面体 
每个面都是直角三角形，故①③④⑤正确，而任取四点构成的平行四边形的两组对边中至少有一组是长方体的平行的一对棱，故这个平行四边形一定是矩形，从而②错误.
所以答案是①③④⑤
【考点精析】通过灵活运用棱柱的结构特征，掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形即可以解答此题．
练习册系列答案
小学课时特训系列答案
相关题目
【题目】下列四个命题中错误的是（ ）
A.在一次试卷分析中，从每个考室中抽取第5号考生的成绩进行统计，不是简单随机抽样
B.对一个样本容量为100的数据分组，各组的频数如下：
区间 | [17，19） | [19，21） | [21，23） | [23，25） | [25，27） | [27，29） | [29，31） | [31，33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的58%
C.设产品产量与产品质量之间的线性相关系数为﹣0.91，这说明二者存在着高度相关
D.通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如表列联表：
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 
，则有99%以上的把握认为“选择过马路方式与性别有关”
