题目内容
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
【答案】(Ⅰ)tanB=2;(Ⅱ)![]()
【解析】
(I)利用正弦定理化简已知条件,求得![]() 的值.
的值.
(II)由![]() 的值求得
的值求得![]() 的值,从而求得
的值,从而求得![]() 的值,利用正弦定理以及三角形的面积公式列方程,由此求得
的值,利用正弦定理以及三角形的面积公式列方程,由此求得![]() 也即
也即![]() 的值.
的值.
(Ⅰ)∵2a=2bcosC+csinB,利用正弦定理可得:2sinA=2sinBcosC+sinCsinB,又sinA=sin(B+C)=sinBcosC+cosBsinC,
化为:2cosB=sinB≠0,∴tanB=2.
(Ⅱ)∵tanB=2,B∈(0,π),可得sinB![]() ,cosB
,cosB![]() .
.
∴sinA=sin(B+C)=sinBcosC+cosBsinC![]() .
.
∴![]() ,可得:a
,可得:a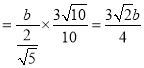 .又
.又![]() absin
absin![]() 6,可得b
6,可得b![]() .
.
∴a![]() ,即
,即![]() ,解得
,解得![]() =
=![]() .
.

练习册系列答案
相关题目