题目内容
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() 射线
射线![]() 交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
(1)求曲线C的直角坐标方程及直线l的参数方程;
(2)当直线l倾斜角α为何值时, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
【答案】(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数))(2)当
为参数))(2)当![]() 时,
时,![]() 取得最小值为
取得最小值为![]()
【解析】
(1)由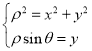 求得曲线
求得曲线![]() 的直角坐标方程;先求出曲线
的直角坐标方程;先求出曲线![]() 与直线
与直线![]() 的交点
的交点![]() 的坐标,即可得到
的坐标,即可得到![]() 的中点
的中点![]() ,进而求解即可;
,进而求解即可;
(2)由(1),将直线![]() 的参数方程代入到曲线
的参数方程代入到曲线![]() 的直角坐标方程中,由参数的几何意义可得
的直角坐标方程中,由参数的几何意义可得![]() ,进而求解即可.
,进而求解即可.
(1)由题,因为![]() ,即
,即![]() ,
,
因为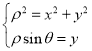 ,
,
所以![]() ,即
,即![]() ,
,
则曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
因为射线![]() 交曲线
交曲线![]() 于点
于点![]() ,所以点
,所以点![]() 的极坐标为
的极坐标为![]() ,
,
则点![]() 的直角坐标为
的直角坐标为![]() ,所以
,所以![]() 的中点
的中点![]() 为
为![]() ,
,
所以倾斜角为![]() 且过点
且过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(2)将直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)代入曲线
为参数)代入曲线![]() 的方程
的方程![]() 中,
中,
整理可得![]() ,
,
设![]() 、
、![]() 对应的参数值分别是
对应的参数值分别是![]() 、
、![]() ,则有
,则有![]() ,
,
则![]() ,
,
因为![]() ,当
,当![]() ,即
,即![]() 时,
时,![]() 取得最小值为
取得最小值为![]()

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目