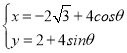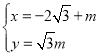题目内容
【题目】椭圆
，椭圆上一点到左焦点的距离的取值范围为
.
（1）求椭圆
的方程；
（2）
，
，
，
分别与椭圆相切，且
，
，
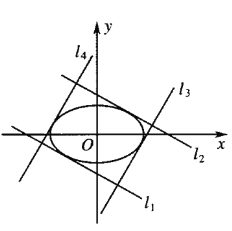
，如图，，，，围成的矩形的面积记为
，求的取值范围.
【答案】（1）
（2）
【解析】
（1）根据椭圆的左、右顶点到椭圆的左焦点的距离分别为最小值和最大值列出方程组，求解即可；
（2）联立直线与椭圆的方程得到一元二次方程，根据韦达定理结合矩形的面积公式得到面积的表达式，结合基本不等式求解面积的取值范围.
（1）因为椭圆上一点到左焦点的距离的取值范围是
，
设椭圆的焦距为
，所以
解得
所以
，故椭圆
的方程为.
（2）当
，
轴或
，
轴时，
；
当，
，，
斜率都存在时，设
，
，
，
，
其中
，且
，
.
将直线的方程与椭圆方程联立得
∴
.
由
，得
，∴
，同理可得
∵
，
，
∴
.
∵，∴
，
∴
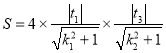
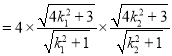
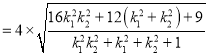
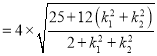
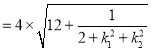，当且仅当
时，等号成立，
∴
∴
，
综上，
灵星计算小达人系列答案
孟建平错题本系列答案
【题目】已知A，B是抛物线
上的两点，且在x轴两侧，若AB的中点为Q，分别过A，B两点作T的切线，且两切线相交于点P.
（1）求证：直线PQ平行于x轴；
（2）若直线AB经过抛物线T的焦点，求
面积的最小值.
【题目】2020年春季，某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车，现有采购成本分别为
万元/辆和
万元/辆的
两款车型，根据以往这两种出租车车型的数据，得到两款出租车车型使用寿命频数表如下：
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
（1）填写下表，并判断是否有
的把握认为出租车的使用寿命年数与汽车车型有关？
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
（2）从
和
的车型中各随机抽取
车，以
表示这
车中使用寿命不低于
年的车数，求的分布列和数学期望；
（3）根据公司要求，采购成本由出租公司负责，平均每辆出租车每年上交公司
万元，其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年，用频率估计每辆出租车使用寿命的概率，分别以这
辆出租车所产生的平均利润作为决策依据，如果你是该公司的负责人，会选择采购哪款车型？
附：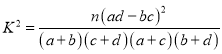
，
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为坚决打赢脱贫攻坚战，某帮扶单位考察了甲乙两种不同的农产品加工生产方式，现对两种生产方式加工的产品质量进行测试并打分对比，得到如下数据：
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 60 | 50 | 30 |
其中产品质量按测试指标可划分为：指标在区间
上的为特优品，指标在区间
上的为一等品，指标在区间
上的为二等品．
（1）用事件
表示“按照生产方式甲生产的产品为特优品”，估计的概率；
（2）填写下面列联表，并根据列联表判断能否有
的把握认为“特优品”与生产方式有关？
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
（3）根据打分结果对甲乙两种生产方式进行优劣比较．
附表：
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式：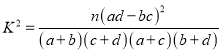
，其中
．
