Question

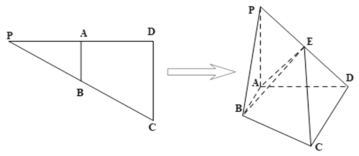
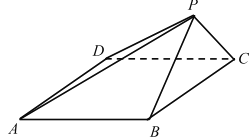
【题目】在四边形ABCD中，BD为四边形的一条对角线，且，将沿BD向上翻折，当点A在平面BCD内的投影恰好为的外心E时，设直线AE与平面ABC，ACD，ABD的夹角分别为，，，则（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

设BC，CD，BD的中点分别为O，P，Q，连接OE，PE，QE，OD，，证明平面AOE，所以平面平面，且平面平面，所以在平面的射影为，即，所以，同理易得，，再根据直线与圆相交的几何性质比较的大小关系，从而得到答案.

设BC，CD，BD的中点分别为O，P，Q，连接OE，PE，QE，，

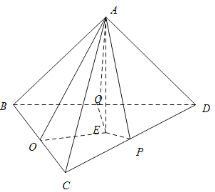
因为点E为的外心，所以，又因为平面BCD，平面BCD，所以，因为，所以平面AOE，所以平面平面，且平面平面，所以在平面的射影为，即，所以，同理易得，，

因为点E为的外心，，，，且，

所以，所以，

易知，，均为锐角，则，

故选：A